Cho tam giác ABC có A=120°.Ba đường phân giác AA',BB',CC'.Chứng minh A'B' vuông góc với A'C'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Ta có AD//CM => ^CAD=^ACM (góc so le trong)
Mà ^BAD=^CAD = ^A/2=120/2=60
=> ^ACM=60
+ Ta có ^CAM=180-^A=180-120=60
=> Trong tam giác ACM có ^AMC=180-(^ACM+^CAM)=180-(60+60)=60
Ta có góc BAD=góc DAC=120:2=60 độ mà dd' // với AD=>dCd'=60 độ
=>góc dCd'=góc ACM=60 độ
Ta có: góc BAC +góc CAM =180 độ
=>góc CAM=60 độ
Ta có: góc CAM+góc ACM+góc AMC=180 độ
=>góc AMC=60 độ

Ta có AA′⊥ AB′ vì chúng là hai tia phân giác của hai góc kề bù. Tương tự AA′⊥ AC′. Vì qua A chỉ có một đường vuông góc với AA' nên ba điểm B', A, C' thẳng hàng và AA′⊥ B′C′, hay A'A là một đường cao của tam giác A'B'C'. Hoàn toàn tương tự ta chứng minh được BB' và CC' là hai đường cao của tam giác A'B'C'.
Mặt khác theo cách chứng minh của bài 9.5 ta có AA', BB', CC' là ba tia phân giác của các góc A, B, C của tam giác ABC. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C'.
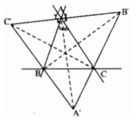


Gọi tia đối AB là Ad, tia đối AC là Ar
-Vì AA' là phân giác của góc BAC nên BAA'=CAA'=120/2=60 độ
-Vì rAB+BAC=180 độ (kề bù) dAC+BAC=180 độ (kề bù) ,mà BAC=120 độ => rAC=dAC=60 độ
- rAB=BAA'=60 độ nên AB là phân giác góc RAA' hay AB là phân giác góc ngoài của tam giác BAC tại đỉnh A
- A'AC=dAC=60 độ nên AC là phân giác góc DAA' hay AC là phân giác góc ngoài của tam giác BAC tại đỉnh A
*Xét tam giác ABA' phân giác BB' cắt phân giác góc ngoài AC tại B' => A'B' là phân giác góc ngoài của tam giác ABA' tại A'
*Xét tam giác ACA' phân giác CC' cắt phân giác góc ngoài AB tại C' => A'C' là phân giác góc ngoài của tam giác ACA' tại A'
+ Từ đó ta có: A'B' và A'C' là phân giác của hai góc kề bù AA'B và AA'C
=> A'B' vuông góc với A'C'
Chúc em hok tốt nha!☘