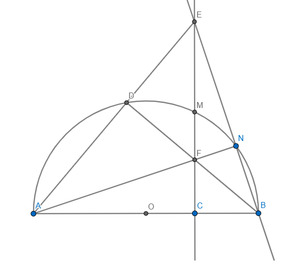
cho đường trong tâm O đường kính AB. Gọi M là điểm trên cung AB sao cho MA bé hơn MB . lấy c thuộc đoạn OB ( C khác O và B). Đường thẳng vuông góc với AB tại C cắt MB tại H. và cắt AM tại điểm E
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì AB là đường kính \(\Rightarrow\angle ANB=90\)
\(\Rightarrow\angle FNB+\angle FCB=90+90=180\Rightarrow BCFN\) nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Xét \(\Delta ACE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle ADB=\angle ACE=90\\\angle BAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AB}\Rightarrow AD.AE=AB.AC\)

a: góc BNA=1/2*180=90 độ
góc FNB+góc FCB=180 độ
=>FCBN nội tiếp
b: góc ADB=1/2*180=90 độ
Xét ΔADB vuông tạiD và ΔACE vuông tại C có
góc A chung
=>ΔADB đồng dạng với ΔACE
=>AD/AC=AB/AE
=>AC*AB=AD*AE
c: Xét ΔEAB có
EC,AN là đường cao
EC cắt AN tại F
=>F là trực tâm
=>BF vuông góc AE
mà BD vuông góc AE
nên B,F,D thẳng hàng

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

1) Vì AB là đường kính \(\Rightarrow\angle ADB=90\) mà \(\angle ECB=90\Rightarrow BCDE\) nội tiếp
2) Vì \(\left\{{}\begin{matrix}EF\bot AB\\AF\bot EB\end{matrix}\right.\Rightarrow F\) là trực tâm tam giác EAB \(\Rightarrow BF\bot AE\)
mà \(BD\bot AE\left(\angle BDA=90\right)\Rightarrow B,F,D\) thẳng hàng
Ta có: \(\angle FNB+\angle FCB=90+90=180\Rightarrow FNBC\) nội tiếp
Xét \(\Delta AFC\) và \(\Delta ABN:\) Ta có: \(\left\{{}\begin{matrix}\angle ACF=\angle ANB=90\\\angle NABchung\end{matrix}\right.\)
\(\Rightarrow\Delta AFC\sim\Delta ABN\left(g-g\right)\Rightarrow\dfrac{AF}{AC}=\dfrac{AB}{AN}\Rightarrow AF.AN=AB.AC\)
Tương tự \(\Rightarrow BF.BD=BC.BA\)
\(\Rightarrow AF.AN+BF.BD=AB.AC+AB.BC=AB^2=4R^2\)
3) Gọi G là giao điểm của (AEF) và AB
Ta có: \(\angle FGB=\angle AEF\left(AEFGnt\right)=\angle DBA\left(BCDEnt\right)\Rightarrow\Delta GFB\) cân tại F có \(FC\bot GB\Rightarrow CB=CG\)
mà C,B cố định \(\Rightarrow G\) cố định
Vì AEFG nội tiếp \(\Rightarrow I\in\) trung trực AG mà A,G cố định \(\Rightarrow\) đpcm

góc ADB=1/2*180=90 độ
góc ANB=góc ADB=90 độ
Xét ΔEAB có
BD,AN,EC là đường cao
BD cắt EC tại F
=>F là trựctâm
góc ADF+góc ACF=180 độ
=>ADFC nội tiếp
góc EDF+góc ENF=180 độ
=>EDFN nội tiếp
góc CDF=góc CAF
góc NDF=góc ECB
mà góc CAF=góc ECB
nên góc CDF=góc NDF
=>DF là phân giác của góc NDC(1)
góc DNF=góc AEC
góc CNF=góc DBA
góc AEC=góc DBA
=>góc DNF=góc CNF
=>NF là phân giác của góc DNC(2)
Từ (1), (2) suy ra F là tâm đường tròn nội tiêp ΔCND

b) Dễ thấy C là trực tâm của tam giác IAB nên C, I, H thẳng hàng.
Do tứ giác AICK là hình thang nội tiếp được đường tròn nên là hình thang cân.
Khi đó \(\widehat{IAK}=\widehat{CKA}\Rightarrow\widehat{IAB}=\widehat{NBA}\)
Suy ra tam giác NAB vuông cân tại N nên \(\widehat{NBA}=45^o\).
Ta có các tứ giác CMIN, AMIH nội tiếp được nên \(\widehat{NMH}=\widehat{NMI}+\widehat{HMI}=\widehat{ICN}+\widehat{IAB}=45^o+45^o=90^o\Rightarrow MN\perp MH\).

c) Đề phải là \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}\ge6\).
Đặt \(x=\dfrac{IH}{CH};y=\dfrac{IN}{AN};z=\dfrac{IM}{BM}\left(x,y,z< 1\right)\).
Ta có \(x+y+z=\dfrac{S_{IAB}}{S_{ABC}}+\dfrac{S_{IBC}}{S_{ABC}}+\dfrac{S_{ICA}}{S_{ABC}}=1\).
Lại có \(\dfrac{IH}{CH}=x\Rightarrow\dfrac{CH}{IH}=\dfrac{1}{x}\Rightarrow\dfrac{IC}{IH}=\dfrac{1}{x}-1\).
Tương tự \(\dfrac{IA}{IN}=\dfrac{1}{y}-1;\dfrac{IB}{IM}=\dfrac{1}{z}-1\).
Do đó \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-3\ge_{Svacxo}\dfrac{9}{x+y+z}-3=\dfrac{9}{1}-3=6\).
Vậy ta có đpcm.

Vì `hat{ACB},hat{ADB}` là 2 góc chẵn nửa (O)
`=>hat{ACB}=hat{ADB}=90^o`
`=>hat{ICM}=hat{IDM}=90^o`
`=>hat{ICM}+hat{IDM}=180^o`
`=>` tg CIDM nt
Vì `MH bot AB`
`=>hat{MHB}=90^o`
`=>hat{MCB}=hat{MHB}=90^o`
`=>` tg CHBD nt (2 đỉnh kề nhau dưới 1 góc không đổi)

Lời giải:
$\widehat{AMB}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow MB\perp AD$
Tam giác $ABD$ có $MB\perp AD, DH\perp AB$ và $MB, DH$ cắt nhau tại $C$ nên $C$ là trực tâm tam giác $ABD$
$\Rightarrow AC\perp BD$
Lấy $E'$ là giao điểm của $AC$ và $BD$ thì $\widehat{AE'B}=90^0$
Như vậy: $\widehat{AMB}=\widehat{AE'B}$ và cùng nhìn cạnh $AB$ nên $AME'B$ là tứ giác nội tiếp
$\Rightarrow E'\in (O)$
Như vậy, $E'\in (O)$ và $E'\in AC$ nên $E'\equiv E$
$\Rightarrow B,E,D$ thẳng hàng.
Ta có: \(\widehat{MOH}=\widehat{MOB}=180^0-2\widehat{MBO}\)
Mặt khác: dễ thấy tứ giác $AMEB, CEBH$ nội tiếp nên: $\widehat{MEH}=\widehat{MEA}+\widehat{CEH}$
$=\widehat{MBA}+\widehat{CBH}=2\widehat{MBO}$
Từ đây suy ra: $\widehat{MOH}+\widehat{MEH}=180^0$
$\Rightarrow MOHE$ là tứ giác nội tiếp.