cho mình hỏi bài này
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ý bạn là \(x-y-z=-33?\)
Ta có \(2x=3y=5z\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x-y-z}{15-10-6}=\dfrac{-33}{-1}=33\\ \Rightarrow\left\{{}\begin{matrix}x=33\cdot15=495\\y=33\cdot10=330\\z=33\cdot6=198\end{matrix}\right.\)

Đổi hỗn số thành phân số
17/7 và 34/21 tỉ số phần trăm là: 150%
Tick nha!! Tks
HT
2 và 3/7=17/7 1 và 13/21 = 34/21
Tỉ số phần trăm là:
17/7:34/21=3/2
3/2=1.5
1.5 =150%
Đáp số : 150 %
Dấu chấm là dấu phẩy đó nha
love you.tick nha

Lời giải:
a.
$xy+x\sqrt{y}-\sqrt{y}-1=x\sqrt{y}(\sqrt{y}+1)-(\sqrt{y}+1)=(\sqrt{y}+1)(x\sqrt{y}-1)$
b.
$ab-a\sqrt{b}+b-\sqrt{b}=(ab+b)-(a\sqrt{b}+\sqrt{b})$
$=b(a+1)-\sqrt{b}(a+1)=(a+1)(b-\sqrt{b})=\sqrt{b}(\sqrt{b}-1)(a+1)$

\(B=\dfrac{\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{7}-1-\sqrt{7}-1}{\sqrt{2}}=-\sqrt{2}\)
B=\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\)
=>\(B^2=4-\sqrt{7}+4+\sqrt{7}-2\sqrt{\left(4-\sqrt{7}\right)\left(4+\sqrt{7}\right)}=8-2\sqrt{16-7}\)
\(B^2=8-2\sqrt{9}=8-2.3=8-6=2\)
\(\Rightarrow B=\sqrt{2}\) hoặc \(B=-\sqrt{2}\)
Vì \(4-\sqrt{7}< 4+\sqrt{7}\Rightarrow\sqrt{4-\sqrt{7}}< \sqrt{4+\sqrt{7}}\)
\(\Leftrightarrow\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}< 0\)
hay B<0=>B=\(-\sqrt{2}\)


Bài 2
9+9.3+18:2.6
=9.4+9.6
=9.(4+6)
=9.10
=90
3.9+18.2+2.9+9
=3.9+9.4+9.3
=9.(3+4+3)
=9.10
=90
44.5+18.10+20.5
=22.10+18.10+10.10
=10.(22+18+10)
=10.50
=500
1.
= 9 + 27 + 9 . 6
= 9 + 27 + 54
= 90
2.
= 27 + 18 . 2 + 2 . 9 + 9
= 27 + 36 + 18 + 9
= 90
3.
= (44 x 5) + (18 x 10) + (20 x 5)
= 220 + 180 + 100
= 500

a,mấy đoạn dấu : dấu+ trong đề hơi khó nhìn
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(P=\left[\dfrac{\sqrt{x}.\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left(\dfrac{\sqrt{x}-1+2}{x-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{x-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{x-1}{\sqrt{x}}\)
b, \(P>0=>\dfrac{x-1}{\sqrt{x}}>0=>x-1>0< =>x>1\)(tm)
Vậy \(x>1\) .....
\(\)

Xét vế trái:
\(x^3+2x=x^3-x+3x=\left(x-1\right)x\left(x+1\right)+3x\)
Do \(\left(x-1\right)x\left(x+1\right)\) là tích 3 số nguyên liên tiếp nên luôn chia hết cho 3
\(\Rightarrow x^3+2x\) chia hết cho 3 với mọi x nguyên
\(y^2\) là bình phương của 1 số nguyên nên chia 3 chỉ có các số dư -1; 0; 1
Mà \(2018\) chia 3 dư 2
\(\Rightarrow2018-y^2\) không chia hết cho 3 với mọi y nguyên
Vậy pt đã cho không có cặp nghiệm nguyên nào thỏa mãn
 Cho mình hỏi bài này.
Cho mình hỏi bài này.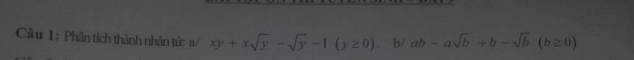 cho mình hỏi bài này
cho mình hỏi bài này
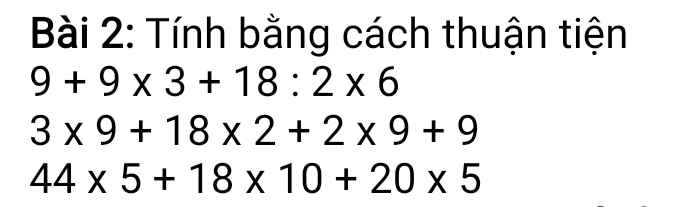


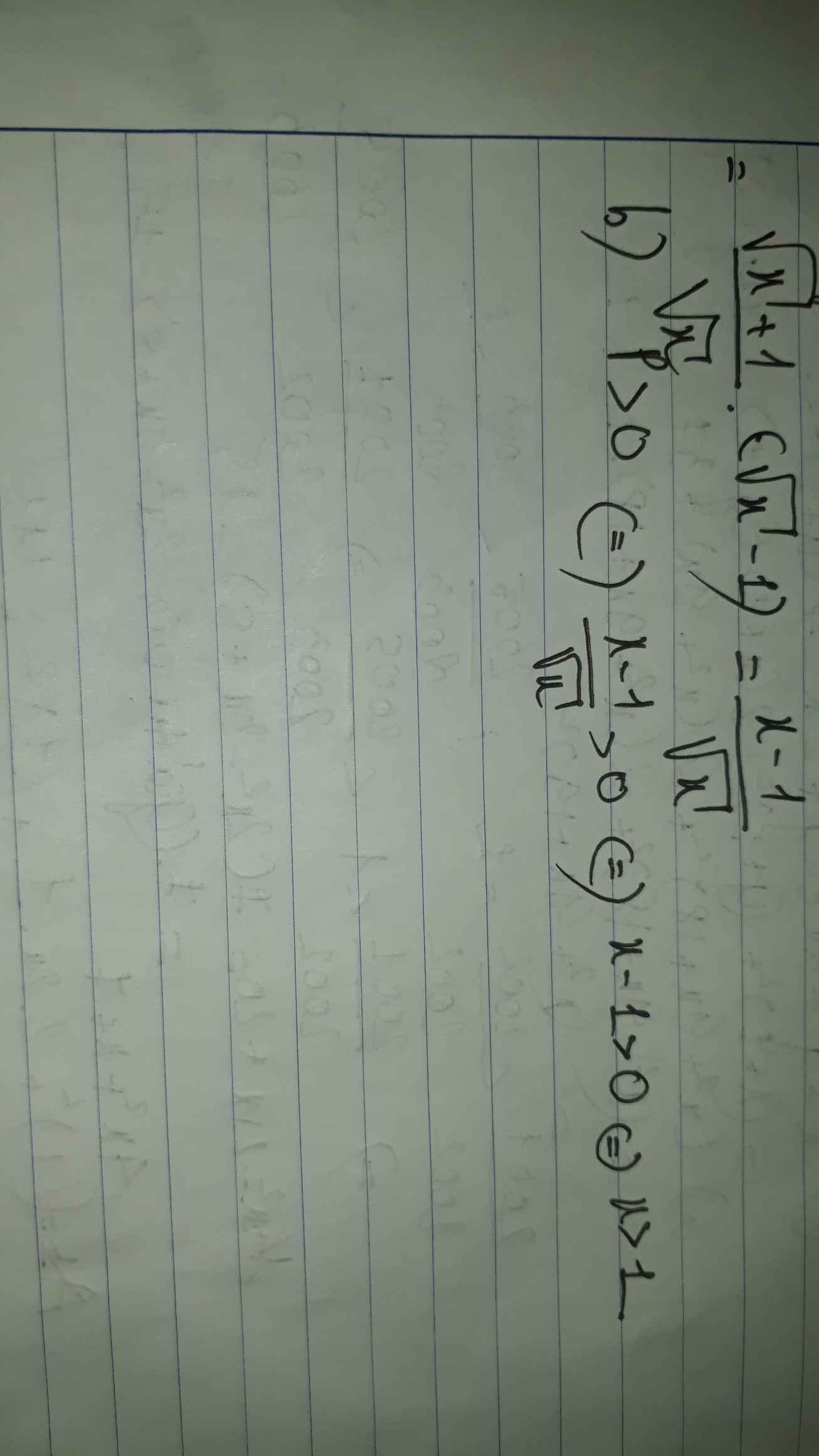

\(A=\sqrt{5}\left(\sqrt{5}-3\right)+\sqrt{45}\)
\(=\sqrt{5}^2-3\sqrt{5}+\sqrt{9.5}\)
\(=\sqrt{5}^2-3\sqrt{5}+3\sqrt{5}\)
\(=\sqrt{5}^2=5\)