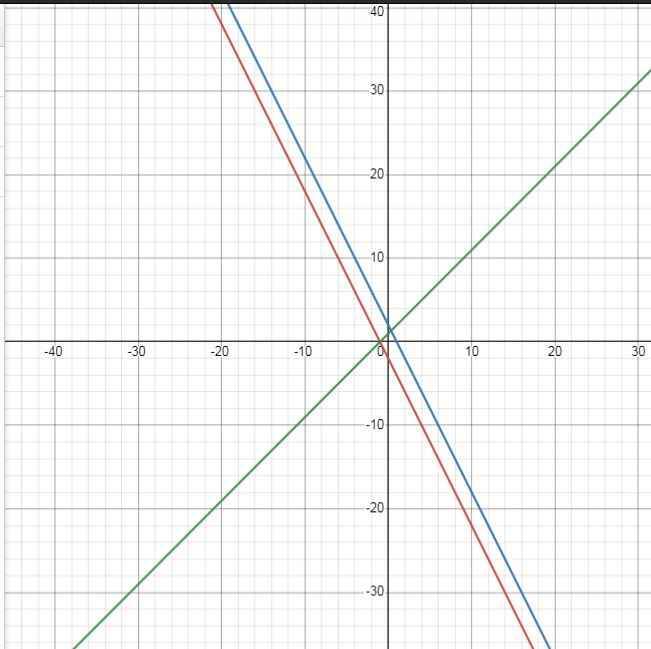
Cho (d1): y= 2x - 1 và (d2): y= -x + 2.
Viết phương trình đường thẳng (d3): y= ax + b biết (d3) cắt Oy tại điểm có tung độ là 3 và thoả điều kiện (d1), (d2), (d3) cùng đi qua một điểm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 12 2021
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-2=-x+1\\y=-x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
MV
20 tháng 12 2021
a)
b, Gọi giao điểm của 2 đường thẳng trên là M(x1;y1)
tọa độ giao điểm của (d1) và (d2) là nghiệm của hpt
<=>
Vậy...
c, phương trình đường thẳng (d3) có dạng y=ax+b
Vì đt(d3) song song với (d2) và cắt đường thẳng (d1) tại một điểm nằm trên trục tung nên ta được a=-1, x=0,y=-7
=> b=-7
Thay a=-1, b=-7 vào cths y=ax+b ta được
y=-x-7
23 tháng 12 2021
\(b,\left(d_3\right)\text{//}\left(d_1\right)\Leftrightarrow\left\{{}\begin{matrix}a=1\\b\ne4\end{matrix}\right.\Leftrightarrow\left(d_3\right):y=x+b\)
PT hoành độ giao điểm \(\left(d_2\right);\left(d_3\right)\) là \(x+b=-2x-2\)
Mà 2 đt cắt tại hoành độ \(-3\) nên \(x=-3\)
\(\Leftrightarrow b-3=4\Leftrightarrow b=7\)
Vậy \(\left(d_3\right):y=x+7\)
24 tháng 11 2021
\(b,\text{PT hoành độ giao điểm: }-2x+5=x-1\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ \text{Vậy }A\left(2;1\right)\text{ là giao điểm }\left(d_1\right)\text{ và }\left(d_2\right)\\ c,\text{Gọi }\left(d_3\right):y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \left(d_3\right)\text{//}\left(d_1\right)\text{ và }M\left(-2;1\right)\in\left(d_3\right)\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne5\\-2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(d_3\right):y=-2x-1\)
14 tháng 11 2021
a, Phương trình hoành độ giao điểm là \(\dfrac{3}{2}x=3x-3\Leftrightarrow\dfrac{3}{2}x=3\Leftrightarrow x=2\Leftrightarrow y=3\Leftrightarrow A\left(2;3\right)\)
Vậy \(A\left(2;3\right)\) là giao điểm của 2 đt
b, Gọi \(\left(d_3\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm
\(\left(d_3\right)//\left(d_1\right)\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b\ne0\end{matrix}\right.\)
PT giao của d3 với Ox tại hoành độ -6 là \(-6a+b=0\Leftrightarrow b=6\cdot\dfrac{3}{2}=9\)
Vậy \(\left(d_3\right):y=\dfrac{3}{2}x+9\)
21 tháng 9 2023
a) \(\left(d_1\right):y=-2x-2\)
\(\left(d_2\right):y=ax+b\)
\(\left(d_2\right)//d_1\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left(d_2\right):y=-2x+b\)
\(M\left(2;-2\right)\in\left(d_2\right)\Leftrightarrow-2.2+b=-2\)
\(\Leftrightarrow b=2\) \(\left(thỏa.đk.b\ne-2\right)\)
Vậy \(\left(d_2\right):y=-2x+2\)
b) \(\left\{{}\begin{matrix}\left(d_1\right):y=-2x-2\\\left(d_2\right):y=-2x+2\end{matrix}\right.\)
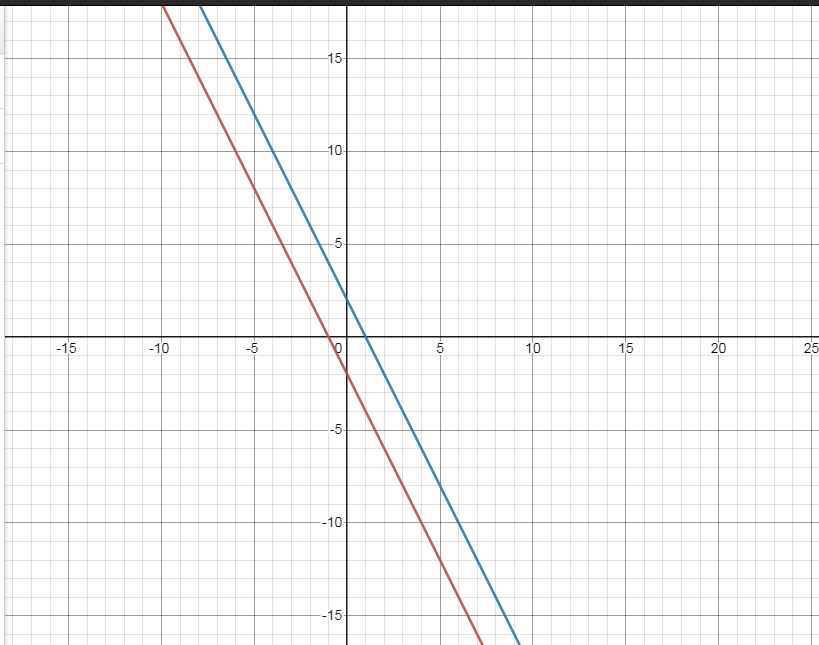
c) \(\left(d_3\right):y=x+m\)
\(\left(d_1\right)\cap\left(d_3\right)=A\left(x;0\right)\Leftrightarrow\left\{{}\begin{matrix}y=x+m\\y=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=x+m\\0=-2x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\x=-1\end{matrix}\right.\)
\(\Rightarrow\left(d_3\right):y=x+1\)
