Cho hình nón có chiều cao bằng 12cm và mặt cắt theo trục của hình nón là 1 tam giác đều. Tính thể tích của hình nón đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
23 tháng 7 2019
Đáp án D
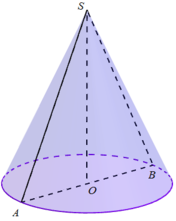
Phương pháp:
Diện tích xung quanh của khối nón: Sxq = πRl
Cách giải:
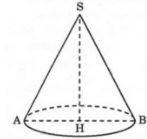
Theo đề bài, ta có tam giác SAB là tam giác vuông cân tại S, SO = a ⇒ R = OA = SO = a


CM
16 tháng 2 2019
Đáp án D
Độ dài đường sinh là: l = a 2 + a 2 = a 2 . Diện tích xung quanh của hình nón là: S x q = π . a . a 2 = 2 π a 2

CM
8 tháng 7 2019
Đáp án B
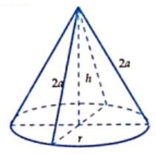
Từ giả thiết ta có thiết diện là tam giác đều cạnh 2r và đường cao h nên ta có:
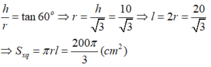
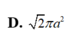
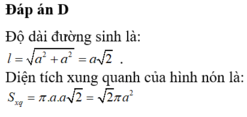
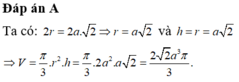


Lời giải:
Gọi độ dài cạnh tam gaics đều là $a$ thì $a$ chính là đường kính đáy hình nón.
Chiều cao (áp dụng định lý Pitago): $\sqrt{a^2-(\frac{a}{2})^2}=\frac{\sqrt{3}}{2}a$
Theo bài ra:
$\frac{\sqrt{3}}{2}a=12\Rightarrow a=8\sqrt{3}$ (cm)
Bán kính đáy: $a:2=4\sqrt{3}$ (cm)
Diện tích mặt đáy: $\pi R^2=(4\sqrt{3})^2\pi =48\pi$ (cm2)
Thể tích: $\frac{1}{3}.48\pi.12=192\pi$ (cm3)