Cho tam giác ABC vuông tại A có góc B=30o và BC = a. Tính AC theo a.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét ΔAMB và ΔEMB có
BA=BE(gt)
\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))
BM chung
Do đó: ΔAMB=ΔEMB(c-g-c)
Suy ra: \(\widehat{MAB}=\widehat{MEB}\)(hai góc tương ứng)
mà \(\widehat{MAB}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{MEB}=90^0\)
hay ME\(\perp\)BC(đpcm)
b) Ta có: ΔABC vuông tại A(gt)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ABC}+30^0=90^0\)
\(\Leftrightarrow\widehat{ABC}=60^0\)
hay \(\widehat{ABE}=60^0\)
Xét ΔABE có BA=BE(gt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Xét ΔBAE cân tại B có \(\widehat{ABE}=60^0\)(cmt)
nên ΔBAE đều(Dấu hiệu nhận biết tam giác đều)

\(AC=\sin B\cdot BC=\dfrac{1}{2}\cdot18=9\left(cm\right)\)

3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

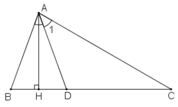
Ta có: ∠(A1 ) =(1/2 )∠(BAC) = (1/2).80o = 40o
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có ∠(ADH) là góc ngoài tại đỉnh D
Do đó: ∠(ADH) = ∠(A1) + ∠C (tính chất góc ngoài của tam giác)
Vậy ∠(ADH ) = 40o + 30o = 70o

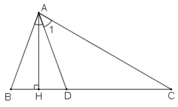
ΔADH vuông tại H nên:
∠(HAD) + ∠(ADH) = 90o (tính chất tam giác vuông)
⇒∠ (HAD) = 90o-∠(ADH)o = 90o - 70o = 20o

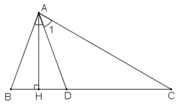
Trong ΔABC có:
∠(BAC) + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Mà ∠(BAC) + 70o + 30o = 180
Vậy ∠(BAC) = 180o-70o - 30o = 80o

a) Xét ΔABC có
\(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{4}{5}\)
nên \(\widehat{C}\simeq53^0\)
\(\Leftrightarrow\widehat{B}=37^0\)
b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{4}=\dfrac{CD}{3}\)
mà BD+CD=5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{4}=\dfrac{CD}{3}=\dfrac{BD+CD}{4+3}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{20}{7}cm;CD=\dfrac{15}{7}cm\)

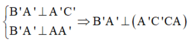
B A C D
Lấy D thuộc tia đối của tia AC sao cho DA = AC
=> BA là trung tuyến của tam giác BDC đồng thời là đường cao
=> tam giác BDC cân tại B
Hơn nữa, tam giác ABC vuông tại A , góc B = 30o
=> gócC = 60o mà tam giác BDC cân tại B
=> tam giác BDC đều
=> DC =BC =a
=> AC= DC/2 = a/2