Cho hình vuông ABCD có AB=a. Gọi M,N lần lượt là 2 điểm tùy ý tren AB,AD sao cho chu vi tam giác AMN=2a. Gọi H là hình chiếu của C trên MN. Chứng minh H luôn thuộc 1 đường tròn cố định khi MN chuyển động trên cạnh AB,AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 7 2018
\(B=1+3+3^2+3^3+...+3^{2018}\)
=> \(3B=3+3^2+3^3+3^4+...+3^{2019}\)
=> \(2B=3B-B=\left(3+3^2+3^3+3^4+...+3^{2019}\right)-\left(1+3+3^2+3^3+...+3^{2018}\right)\)
=> \(2B=3^{2019}-1\)
=> \(B=\frac{3^{2019}-1}{2}\)
CM
22 tháng 9 2017
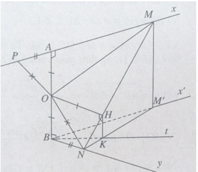
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
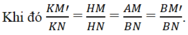
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)
H
22 tháng 3 2018
Tự vẽ hình nha,
Câu a, Ta có : tứ giác AHMK là hình chữ nhật nên MK=AH và HM=AK
Mà HM, MK lần lượt là bán kính của (H) và (M)
Xét tam giác HAK có : theo bđt tam giác : HA-HB<HK<HA+HK
Hay MK-MH<HK<MH+MK => hai đường tròn luôn cắt nhau ( giả sử MK>MH)
28 tháng 3 2018
Ta có \(\widehat{NMH}=\widehat{NCB};\widehat{NMK}=\widehat{NBC}\)
Do AKMH là hình chữ nhật nên
\(\widehat{NMH}+\widehat{NMK}=90\Rightarrow\widehat{NCB}+\widehat{NBC}=90\)
\(\Rightarrow\widehat{BNC}=90\). Vẽ hình vuông ABEC
Ta có A, N, B, E, C cùng thuộc đường tròn đường kính BC cố định
Ta lại có \(\widehat{NEB}=\widehat{NCB}\)mà \(\widehat{NCB}=\widehat{NMH}\)
\(\widehat{NEB}=\widehat{NMH}\), do \(MH//EB\)nên ba điểm N, M, E thẳng hàng. Vậy MN luôn đi qua điểm E cố định