Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

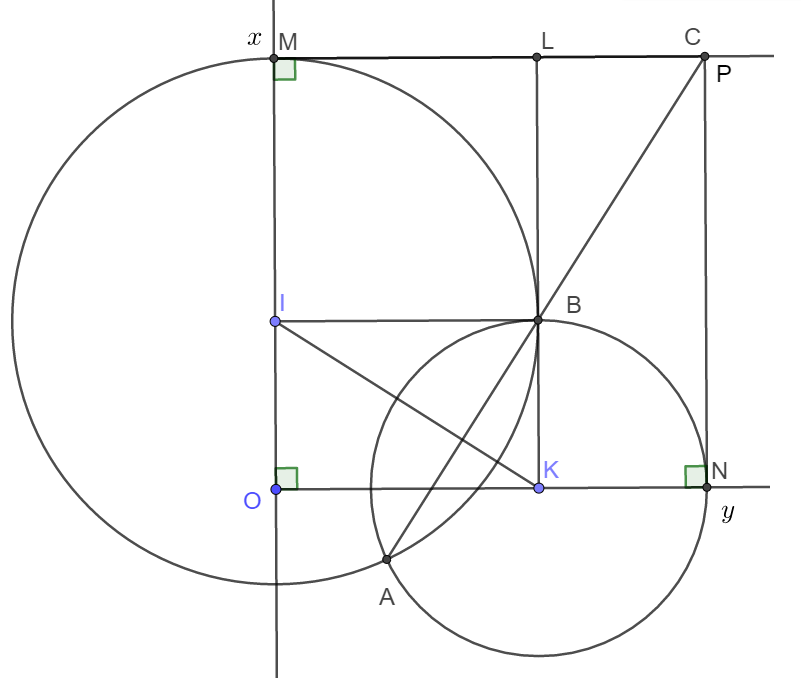
a) Trong tam giác OIK có:
|OK −− OI| < IK < |OK + OI| hay ∣R−r∣<IK<∣R+r∣∣R−r∣<IK<∣R+r∣.
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra ΔBLP=ΔKOIΔBLP=ΔKOI. Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.

Tự vẽ hình nha,
Câu a, Ta có : tứ giác AHMK là hình chữ nhật nên MK=AH và HM=AK
Mà HM, MK lần lượt là bán kính của (H) và (M)
Xét tam giác HAK có : theo bđt tam giác : HA-HB<HK<HA+HK
Hay MK-MH<HK<MH+MK => hai đường tròn luôn cắt nhau ( giả sử MK>MH)
Ta có \(\widehat{NMH}=\widehat{NCB};\widehat{NMK}=\widehat{NBC}\)
Do AKMH là hình chữ nhật nên
\(\widehat{NMH}+\widehat{NMK}=90\Rightarrow\widehat{NCB}+\widehat{NBC}=90\)
\(\Rightarrow\widehat{BNC}=90\). Vẽ hình vuông ABEC
Ta có A, N, B, E, C cùng thuộc đường tròn đường kính BC cố định
Ta lại có \(\widehat{NEB}=\widehat{NCB}\)mà \(\widehat{NCB}=\widehat{NMH}\)
\(\widehat{NEB}=\widehat{NMH}\), do \(MH//EB\)nên ba điểm N, M, E thẳng hàng. Vậy MN luôn đi qua điểm E cố định