A B C H 1 2 Chứng minh góc B = góc...
Đọc tiếp
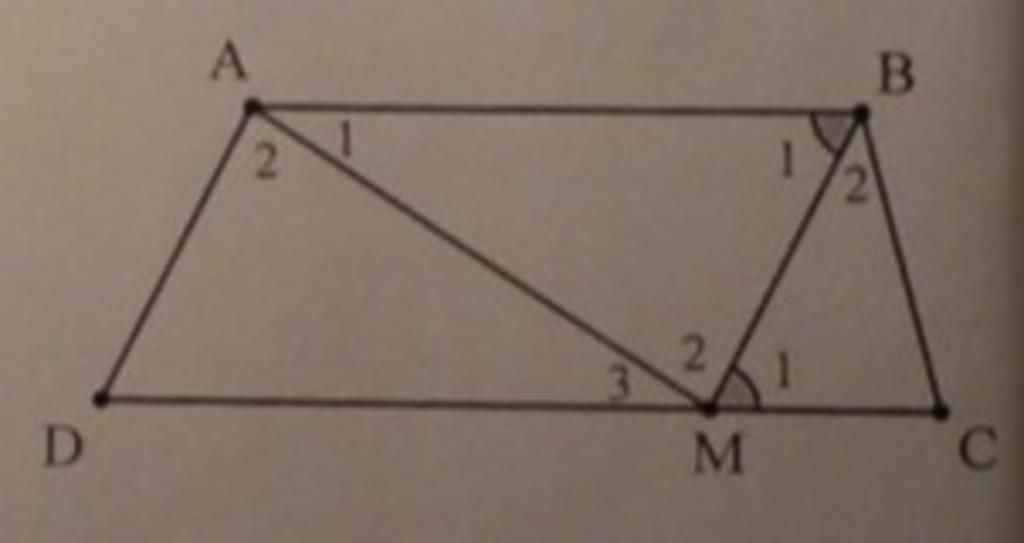
Chứng minh góc B = góc A2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 12 2021
Bài 8. Cho x và y là hai đại lượng tỉ lệ nghịch. Gọi 1 2 x x; là hai giá trị của x và 1 2 y y; là hai giá trị tương ứng của y . Biết rằng 1 2 x x 5 39 và 1 2 y y 8; 12, hãy: a. Tính 1 2 x x; . b. Biểu diễn y theo x .
CM
3 tháng 4 2019
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
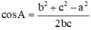
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
HA
1
29 tháng 7 2023
a: Xét ΔABC có AC>AB
nên góc B>góc C
b: Xét ΔABC có AB<AC
mà HB,HC lần lượt là hình chiếu của AB,AC trên BC
nên HB<HC
c: góc B+góc C=90 độ
góc HAC+góc C=90 độ
=>góc B=góc HAC
góc C+góc B=90 độ
góc HAB+góc B=90 độ
=>góc C=góc HAB
9 tháng 10 2021
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK
MQ
0
bn cho thêm đk đi ko đủ nha