tìm điều kiện xác định của \(\sqrt{-4x^2+4x-1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ĐKXĐ:
$\begin{cases}1-2x\ge 0\\3-4x\ge 0\end{cases}\\\Leftrightarrow \begin{cases}2x\le 1\\4x\le 3\end{cases}\\\Leftrightarrow \begin{cases}x\le \dfrac{1}{2}\\x\le \dfrac{3}{4}\end{cases}\\\Leftrightarrow x\le \dfrac{1}{2}$
b) ĐKXĐ:
$\begin{cases}1+x\ge 0\\-4x\ge 0\end{cases}\\\Leftrightarrow \begin{cases}x\ge -1\\x\le 0\end{cases}\\\Leftrightarrow-1\le x\le 0$

\(ĐK:4x^2-12x+9=\left(2x-3\right)^2\ge0\) (luôn đúng) hay \(ĐK:x\in R\)

\(a,ĐK:2-x^2\ge0\Leftrightarrow x^2\le2\Leftrightarrow-\sqrt{2}\le x\le\sqrt{2}\\ b,ĐK:5x^2-3>0\Leftrightarrow x^2>\dfrac{3}{5}\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{\sqrt{15}}{5}\\x< -\dfrac{\sqrt{15}}{5}\end{matrix}\right.\\ c,ĐK:-\left(2x-1\right)^2\ge0\Leftrightarrow x=\dfrac{1}{2}\\ d,ĐK:x^2+x-2>0\\ \Leftrightarrow\left(x-1\right)\left(x+2\right)>0\\ \Leftrightarrow\left[{}\begin{matrix}x>1\\x< -2\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}x^2-4x+2\ge0\\x-2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge2+\sqrt{2}\\x\le2-\sqrt{2}\end{matrix}\right.\\x\ge2\end{matrix}\right.\)
\(\Rightarrow x\ge2+\sqrt{2}\)
\(x^2-4x+2\ge0\Leftrightarrow x^2-4x+4\ge2\)
\(\Leftrightarrow\left(x-2\right)^2\ge2\)
\(\Leftrightarrow\left|x-2\right|\ge\sqrt{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2\ge\sqrt{2}\\x-2\le-\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge2+\sqrt{2}\\x\le2-\sqrt{2}\end{matrix}\right.\)

Mình làm thử, bạn xem có đúng hông nha!
\(ĐKXĐ:\hept{\begin{cases}4x+2\ge0\\x^2+4x+1\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge-\frac{1}{2}\\\left(x+2\right)^2-3\ge-3\Leftrightarrow x=-2\end{cases}\Leftrightarrow}x\ge-\frac{1}{2}}\)
Mình giải thử lun nha!
\(\sqrt{4x+2}=\sqrt{x^2+4x+1}\) (1)
Bình phương cả 2 vế của pt, ta được:
\(\left(1\right)\Leftrightarrow\left(\sqrt{4x+2}\right)^2=\left(\sqrt{x^2+4x+1}\right)^2\)
\(\Leftrightarrow4x+2=x^2+4x+1\)
\(\Leftrightarrow x^2-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x-1=0\\x+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\left(\text{nhận }\right)\\x=-1\left(\text{loại}\right)\end{cases}}}\)
Vậy: \(S=\left\{1\right\}\)
(Nếu đúng thì tíck cho mìk vs nhé!)

đkxđ:
\(x^2-4x+3\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x-3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x-3\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge3\\x\le1\end{matrix}\right.\)
Vậy đkxđ của biểu thức là \(\left[{}\begin{matrix}x\ge3\\x\le1\end{matrix}\right.\)
đkxđ:
�2−4�+3≥0x2−4x+3≥0
⇔(�−1)(�−3)≥0⇔(x−1)(x−3)≥0
⇔[{�−1≥0�−3≥0{�−1≤0�−3≤0⇔{x−1≥0x−3≥0{x−1≤0x−3≤0
⇔[�≥3�≤1⇔[x≥3x≤1
Vậy đkxđ của biểu thức là [�≥3�≤1[x≥3x≤1

a: ĐKXĐ: (x-1)(x-3)>=0
=>x>=3 hoặc x<=1
b: ĐKXĐ: (x-4)(x-3)>=0
=>x>=4 hoặc x<=3
c: ĐKXĐ: (x-5)(x-4)>=0
=>x>=5 hoặc x<=4

\(\sqrt{4x^2-4x+1}=0\Rightarrow\sqrt{\left(2x-1\right)^2}=0\Rightarrow2x-1=0\Rightarrow x=\frac{1}{2}\)
Vậy ĐKCĐ: \(x\ge\frac{1}{2}\)
\(A=\frac{\sqrt{4x^2-4x+1}}{4x^2-1}=\frac{\sqrt{\left(2x-1\right)^2}}{4x^2-1}=\frac{2x-1}{\left(2x-1\right)\left(2x+1\right)}=\frac{1}{2x+1}\)
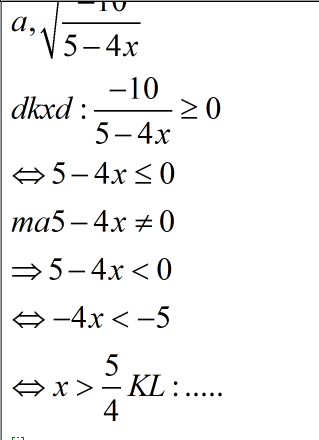
-4x2 + 4x - 1 = -[(2x)2 - 2.2x.1 + 12] = -(2x - 1)2.
-(2x - 1)2 \(\ge0\)(biểu thức lấy căn) mà -(2x - 1)2\(\le0\)(vì\(\left(2x-1\right)^2\ge0\))
\(\Rightarrow-\left(2x-1\right)^2=0\Rightarrow2x-1=0\Rightarrow x=0,5\)