\(x^2+2\sqrt{2}x+2\) phân tích thành nhân tử
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x+3\sqrt{x+2}-2\)
\(=x+2+3\sqrt{x+2}-4\)
\(=\left(\sqrt{x+2}\right)^2+4\sqrt{x+2}-\sqrt{x+2}-4\)
\(=\left(\sqrt{x+2}+4\right)\left(\sqrt{x+2}-1\right)\)
\(x+3\sqrt{x+2}-2=x+2+3\sqrt{x+2}-4\)
\(=x+2-\sqrt{x+2}+4\sqrt{x+2}-4\)
\(=\sqrt{x+2}\left(\sqrt{x+2}-1\right)+4\left(\sqrt{x+2}-1\right)\)
\(=\left(\sqrt{x+2}-1\right)\left(\sqrt{x+2}+4\right)\)

\(x+2\sqrt{x-1}=\left(x-1\right)+2\sqrt{x-1}+1=\left(\sqrt{x-1}+1\right)^2\)
\(x-4\sqrt{x-2}+2=\left(x-2\right)-4\sqrt{x-2}+4=\left(\sqrt{x-2}-2\right)^2\)
\(x+2\sqrt{x-1}=\left(\sqrt{x-1}+1\right)^2\)
\(x-4\sqrt{x-2}+2=\left(\sqrt{x-2}+4\right)^2\)

Lời giải:
$x-2\sqrt{x}-15=(x-5\sqrt{x})+(3\sqrt{x}-15)$
$=\sqrt{x}(\sqrt{x}-5)+3(\sqrt{x}-5)=(\sqrt{x}-5)(\sqrt{x}+3)$

\(1,=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-y-1\right)\left(x+y-1\right)\\ 2,=\left(x+y\right)^3\\ 3,=\left(2y-z\right)\left(4x+7y\right)\\ 4,=\left(x+2\right)^2\\ 5,Sửa:x\left(x-2\right)-x+2=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)

a, \(\dfrac{x^2}{4}-xy+y^2=\left(\dfrac{x}{2}\right)^2-xy+y^2=\left(\dfrac{x}{2}\right)^2-2.\dfrac{x}{2}.y+y^2\)
\(=\left(\dfrac{x^2}{2}-y\right)^2\)
b, \(x^2+x+\dfrac{1}{4}=x^2+\dfrac{1}{2}.2.x+\left(\dfrac{1}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2\)
c, \(x^2+2\sqrt{3}x+3=x^2+2\sqrt{3}x+\left(\sqrt{3}\right)^2=\left(x+\sqrt{3}\right)^2\)
d, \(4x^2-1=\left(2x-1\right)\left(2x+1\right)\)
`x^2/4-2*x/2*y+y^2`
`=(x/2-y)^2`
`x^2+x+1/4`
`=x^2+2*x*1/2+(1/2)^2`
`=(x+1/2)^2`
`x^2+2sqrt3x+3`
`=x+2xsqrt3+sqrt3^2`
`=(x+sqrt3)^2`
`4x^2-1`
`=(2x)^2-1`
`=(2x-1)(2x+1)`

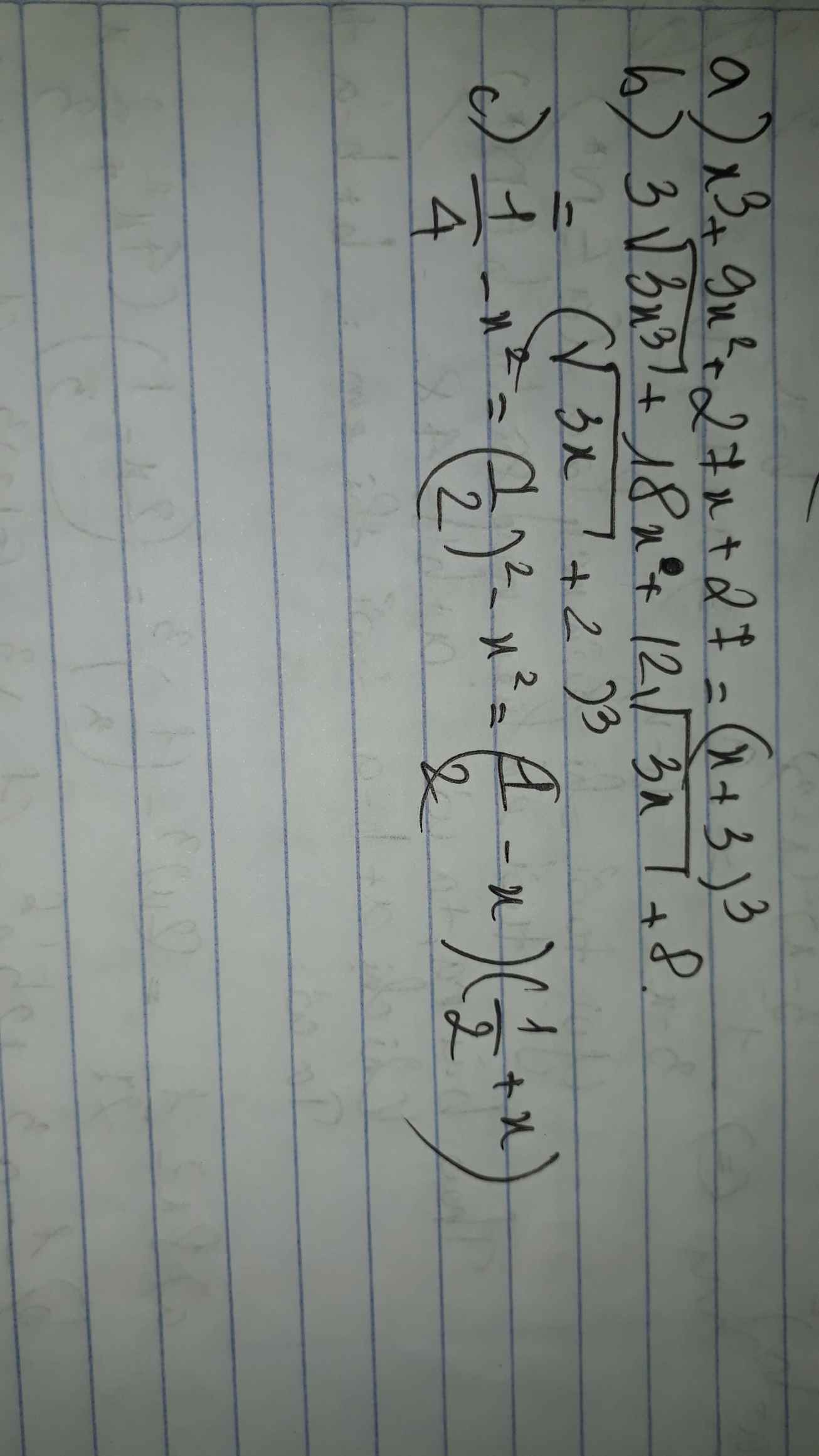
\(=\left(x+\sqrt{2}\right)^2\)
(x+√2)^2