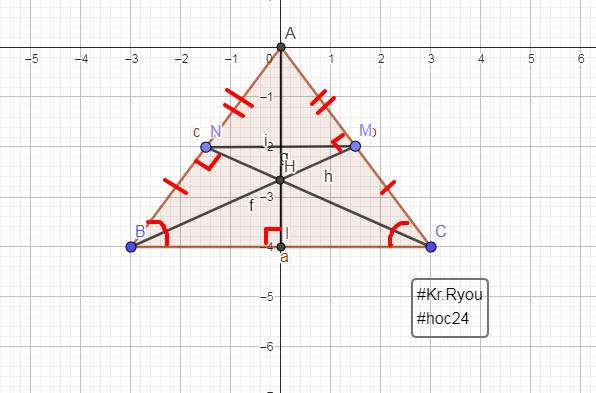
Cho tam giác ABC ccân tại A,kẻ hai đường phân giác BM và CN cắt nhau tại G.Chứng minh rằng:
1)Tam giác ABM= tam giác ACN
2)Tam giác BMC=Tam giác CNB
3)Tam giác GNB=Tam giác GMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2022
1: Xét ΔABM vuông tại M và ΔACN vuông tại N có
AB=AC
góc BAM chung
Do đó: ΔABM=ΔACN
2: XétΔBMC vuông tại M và ΔCNB vuông tại N có
BC chung
BM=CN
Do đó: ΔBMC=ΔCNB
9 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`1)`
Vì `\Delta ABC` cân tại A.
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABM` và `\Delta ACN`:
`\text {AB = AC}`
$\widehat {A} \text { chung}$
$\widehat {ANC} = \widehat {AMB} (=90^0)$
`=> \Delta ABM = \Delta ACN (ch-gn)`
`2)`
Xét `2 \Delta` vuông `BMC` và `CNB`:
$\widehat {B} = \widehat {C}$
`\text {BC chung}`
`=> \Delta BMC = \Delta CNB (ch-gn)`
`3)`
Vì `\Delta BMC = \Delta CNB (b)`
`-> \text {BN = CM (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{AB = AN + NB}\\\text{AC = AM + MC}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BN = CM}\end{matrix}\right.\)
`-> \text {AM = AN}`
Xét `\Delta AMN`:
`\text {AM = AN}`
`-> \Delta AMN` cân tại A.
`4)`
Kẻ đường cao AI
Vì AI đi qua MN
`-> \text {AI} \bot \text {MN}`
Ta có: \(\left\{{}\begin{matrix}\text{AI }\bot\text{ MN}\\\text{AI }\bot\text{ BC}\end{matrix}\right.\)
`@` Theo tiên đề euclid
`-> \text {MN // BC}`
Hoặc bạn có thể giải cách này
Vì `\Delta AMN` cân tại A
\(\rightarrow\widehat{\text{AMN}}=\widehat{\text{ANM}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(1)`
Vì `\Delta ABC` cân tại A
\(\rightarrow\widehat{\text{ABC}}=\widehat{\text{ACB}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(2)`
Từ `(1)` và `(2)`
`->` \(\widehat{\text{ABC}}=\widehat{\text{ANM}}\)
Mà `2` góc này ở vị trí sole trong
`-> \text {MN // BC (t/c 2 đt' //).}`
9 tháng 6 2023
1: Xét ΔABM vuông tại M và ΔACN vuông tại N có
AB=AC
góc BAM chung
=>ΔABM=ΔACN
2: Xét ΔNBC vuông tại N và ΔMCB vuông tại M có
BC chung
góc NBC=góc MCB
=>ΔNBC=ΔMCB
3: Xét ΔAMN có AM=AN
nên ΔAMN cân tại A
4: AM/AC=AN/AB
=>MN//BC
1 tháng 8 2023
a: Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
góc BAM chung
=>ΔAMB=ΔAMC
=>góc ABM=góc ACN
b: góc ABM+góc HBC=góc ABC
góc ACN+góc HCB=góc ACB
mà góc ABM=góc ACN và góc ABC=góc ACB
nên góc HBC=góc HCB
=>HB=HC
c: Xét ΔABC có AN/AB=AM/AC
nên NM//BC
NM//BC
=>góc HMN=góc HBC; góc HNM=góc HCB
mà góc HBC=góc HCB
nên góc HMN=góc HNM
góc EMN=góc MNC
góc MNC=góc HMB
=>góc EMN=góc HMB
=>MN là phân giác của góc EMB
1 tháng 8 2023
a: Xét ΔAMB vuông tại M và ΔANC vuông tại N có AB=AC
góc BAM chung
=>ΔAMB=ΔAMC
=>góc ABM=góc ACN
b: góc ABM+góc HBC=góc ABC
góc ACN+góc HCB=góc ACB
mà góc ABM=góc ACN và góc ABC=góc ACB
nên góc HBC=góc HCB
=>HB=HC
c: Xét ΔABC có AN/AB=AM/AC nên NM//BC NM//BC
=>góc HMN=góc HBC; góc HNM=góc HCB mà góc HBC=góc HCB nên:
góc HMN=góc HNM; góc EMN=góc MNC; góc MNC=góc HMB
=>góc EMN=góc HMB
=>MN là phân giác của góc EMB
18 tháng 4 2016
Bạn tự vẽ hình nha!
a.
AB = AC (tam giác ABC cân tại A)
mà AB = 15 nên AC = 15
Tam giác ABC có:
AC < BC (15 < 18)
=> B < A (quan hệ giữa góc và cạnh đối diện)
b.
Xét tam giác ABH và tam giác ACH có:
A1 = A2 (AH là tia phân giác của BAC)
AB = AC (tam giác ABC cân tại A)
B = C (tam giác ABC cân tại A)
=> Tam giác ABH = Tam giác ACH (g.c.g)
c.
AH là tia phân giác của tam giác ABC cân tại A
=> AH là trung tuyến của tam giác ABC
mà BD là trung tuyến của tam giác ABC
=> G là trọng tâm của tam giác ABC.
d.
AH là tia phân giác của tam giác ABC cân tại A
=> AH là trung trực của tam giác ABC
=> H là trung điểm của BC
=> BH = CH = BC/2 = 18/2 = 9
Áp dụng định lí Pytago vào tam giác ABH vuông tại H có:
AB^2 = AH^2 + BH^2
15^2 = AH^2 + 9^2
AH = 12
Ta có:
AG = 2/3 AH (tính chất trọng tâm)
=> AG = 2/3 . 12 = 8
d.
G là trọng tâm của tam giác ABC
=> CE là trung tuyến của tam giác ABC
=> E là trung điểm của AB
=> AE = BE = AB/2
Ta có: AD = CD = AC/2 (BD là trung tuyến của tam giác ABC)
mà AB = AC (tam giác ABC cân tại A)
=> AE = AD
Xét tam giác AEG và tam giác ADG có:
AE = AD (chứng minh trên)
A1 = A2 (AH là tia phân giác của tam giác ABC)
AG là cạnh chung
=> Tam giác AEG = Tam giác ADG
28 tháng 7 2023
a: Xét ΔABM vuông tại M và ΔACN vuông tại N có
góc BAM chung
=>ΔABM đồng dạng với ΔACN
=>AM/AN=AB/AC
=>AM*AC=AN*AB và AM/AB=AN/AC
b: Xét ΔAMN và ΔABC có
AM/AB=AN/AC
góc MAN chung
=>ΔAMN đòng dạng với ΔABC
c: ΔAMN đồng dạng với ΔABC
=>S AMN/S ABC=(AM/AB)^2=(cos60)^2=1/4
=>S ABC=4*S AMN
25 tháng 2 2022
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔADH vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADH}=\widehat{EDC}\)
Do đó: ΔADH=ΔEDC
c: Xét ΔAHC vuông tại A và ΔECH vuông tại E có
CH chung
AH=EC
Do đó: ΔAHC=ΔECH
1: Xét ΔABM và ΔACN có
\(\widehat{ABM}=\widehat{ACN}\)
AB=AC
góc A chung
Do đó: ΔABM=ΔACN
2: Xét ΔBMC và ΔCNB có
BM=CN
BC chung
MC=NB
Do đó: ΔBMC=ΔCNB