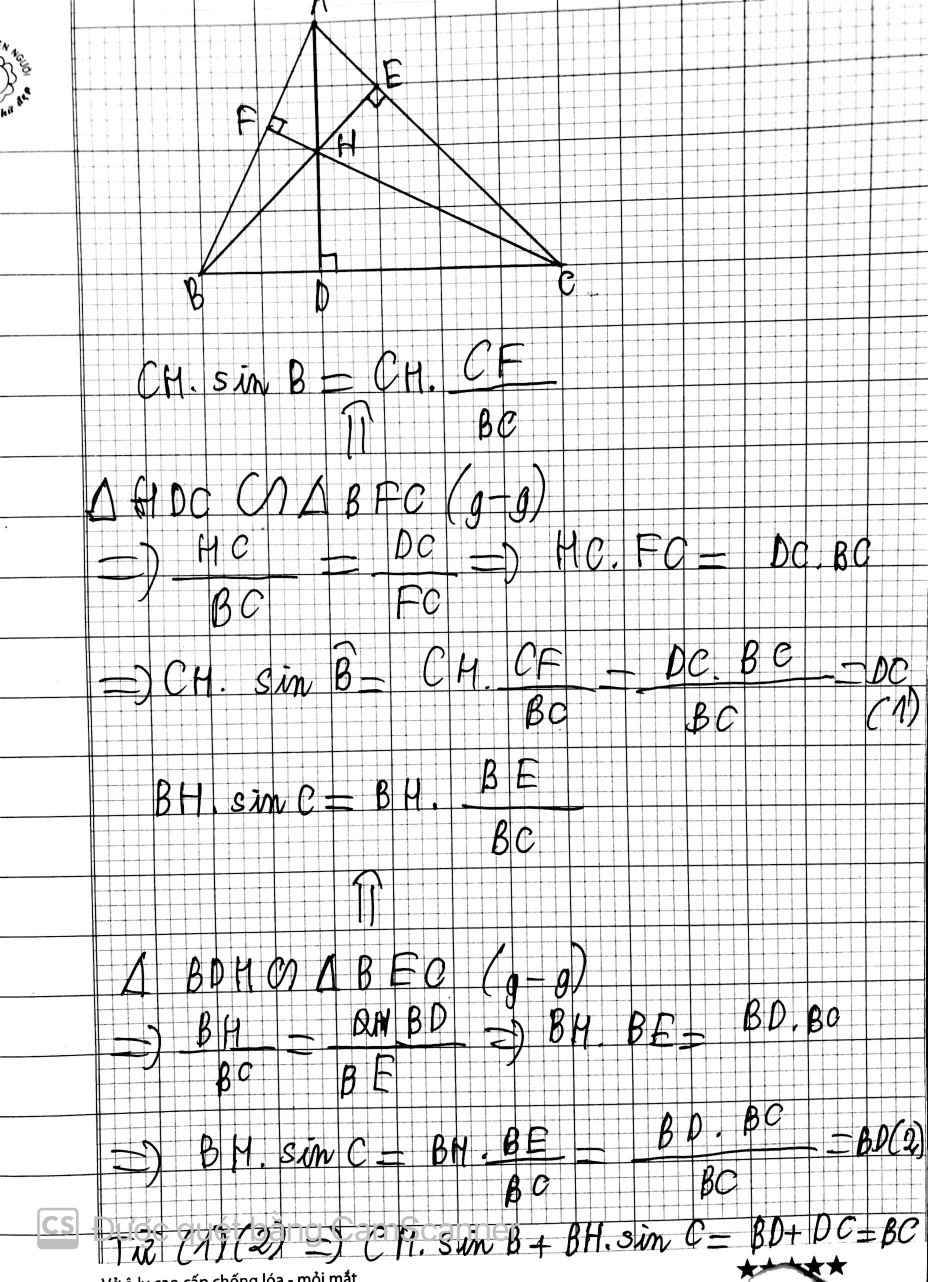Giúp tớ với: Cho tam giác ABC, H là trực tâm. C/m CH.sinB+BH.sinC=bc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
RN
0
TT
0
TP
1
TP
7 tháng 8 2023
a) Chứng minh BH//CD và BH=CD:
Vì O là giao điểm 3 đường trung trực nên O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì A>90 nên tâm đường tròn ngoại tiếp tam giác ABC nằm ngoài tam giác ABC.
Vì H là trực tâm nên AH ⊥ BC và AH cắt BC tại D.
Vì O là trung điểm AD nên OD = AO.
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên OB = OC.
Từ đó suy ra OB = OC = OD = AO.
Vậy tứ giác OBCD là tứ giác nội tiếp.
Do đó, ta có: (BHCD) => ∠BHC + ∠BDC = 180°
Mà ∠BHC + ∠BDC = 90° + 90° = 180°
Vậy BH // CD và BH = CD.
b) Chứng minh M là trung điểm HD:
Vì OM ⊥ BC và H là trực tâm nên HM // BC.
Vì HM // BC và BH // CD nên HM // CD.
Do đó, ta có: (HMD) => ∠HMD + ∠HCD = 180°
Mà ∠HMD + ∠HCD = 90° + 90° = 180°
Vậy HM // CD và HM = CD/2.
Do đó, M là trung điểm HD.
c) Chứng minh H, G, O thẳng hàng:
Gọi E, F lần lượt là trung điểm của AB, AC.
Ta có: EG // HO và EG = (2/3)HO
Do đó, ta có: H, G, O thẳng hàng.
4 tháng 8 2023
tại sao lại là "Vì H là trực tâm nên AH ⊥ BC và AH cắt BC tại D." ạ
"H là trực tâm" rồi mà
18 tháng 7 2021
a) Vì M đối xứng với H qua BC nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM(cmt)
CH=CM(cmt)
BC chung
Do đó: ΔBHC=ΔBMC(c-c-c)
3 tháng 4 2023
a: OM//AH
ON//BH
MN//AB
=>góc BAH=góc OMN và góc ABH=góc ONM
=>ΔABH đồng dạng vơi ΔMNO
b: G là trọng tâm của ΔABC
=>GM/GA=1/2
ΔABH đồng dạng với ΔMNO nên OM/AH=MN/AB=1/2
=>OM/AH=MG/AG
=>ΔHAG đồng dạng với ΔOMG
c: ΔHAG đồng dạng với ΔOMG
=>góc AGH=góc OGM
=>H,G,O thẳng hàng
3 tháng 4 2023
a: OM//AH
ON//BH
MN//AB
=>góc BAH=góc OMN và góc ABH=góc ONM
=>ΔABH đồng dạng với ΔMNO
b: A,G,M thẳng hàng và H,G,O thẳng hàng
=>góc AGH=góc MGO
=>ΔAHG đồng dạng với ΔMOG
=>OM/AH=MG/AG
=>OM/AH=MN/AB=1/2
=>GM/GA=1/2
=>G là trọng tâm của ΔACB