cho tam giác DEF,điểm I nằm trong tam giác và cách đều ba cạnh của nó.Chứng minh I là điểm chung của ba đường phân giác của tam giác DEF
/GIÚP MÌNH VỚI\
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 9 2018
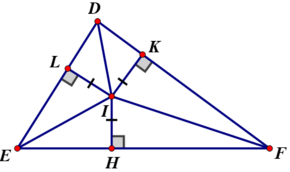
Gọi IH, IK, IL lần lượt là khoảng cách từ I đến EF, DF, DE.
Theo đề bài, điểm I cách đều ba cạnh của ΔDEF ⇒ IH = IK = IL
IL = IK ⇒ I cách đều hai cạnh của góc D ⇒ I nằm trên đường phân giác của góc D.
IH = IK ⇒ I cách đều hai cạnh của góc F ⇒ I nằm trên đường phân giác của góc F.
IH = IL ⇒ I cách đều hai cạnh của góc E ⇒ I nằm trên đường phân giác của góc E.
Từ 3 điều trên suy ra I là điểm chung của ba đường phân giác của tam giác DEF.
19 tháng 4 2017
Hướng dẫn:
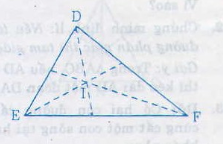
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc ˆDD^, ˆEE^, ˆFF^
Vậy I là điểm chung của ba đường phân giác của tam giác DEF
19 tháng 4 2017
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc , ,
Vậy I là điểm chung của ba đường phân giác của tam giác DEF
27 tháng 8 2016
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc ∠D, ∠E , ∠F
Vậy I là điểm chung của ba đường phân giác của tam giác DEF
27 tháng 8 2016
mà hình như là đại học sư phạm rồi mà.bài dễ thế mà không biết làm à
CM
25 tháng 1 2017
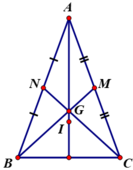
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà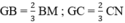 
(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
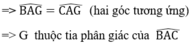
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của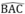 
Vì G, I cùng thuộc tia phân giác của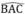 
nên A, G, I thẳng hàng
CM
11 tháng 1 2019
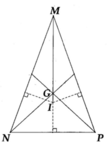
I nằm trong tam giác và cách đều ba cạnh của tam giác nên MI là tia phân giác của góc M.
Do tam giác MNP cân tại M nên đường giác MI cũng là đường trưng tuyến.
G là trọng tâm của tam giác MNP nên G nằm trên MI.
Từ đó, suy ra M,G, I thẳng hàng.
Kẻ IA⊥ED tại A, IB⊥EF tại B, IC⊥DF tại C
Vì I cách đều ba cạnh nên IA=IB=IC
Xét ΔIAE vuông tại A và ΔIBE vuông tại B có
IE chung
IA=IB(cmt)
Do đó: ΔIAE=ΔIBE(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{AEI}=\widehat{BEI}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{DEI}=\widehat{FEI}\)
hay EI là tia phân giác của \(\widehat{DEF}\)(1)
Xét ΔICF vuông tại C và ΔIBF vuông tại B có
IF chung
IC=IB(cmt)
Do đó: ΔICF=ΔIBF(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BFI}=\widehat{CFI}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{EFI}=\widehat{DFI}\)
hay FI là tia phân giác của \(\widehat{EFD}\)(2)
Xét ΔDAI vuông tại A và ΔDCI vuông tại C có
DI chung
IA=IC(cmt)
Do đó: ΔDAI=ΔDCI(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ADI}=\widehat{CDI}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{EDI}=\widehat{FDI}\)
hay DI là tia phân giác của \(\widehat{EDF}\)(3)
Từ (1), (2) và (3) suy ra I là điểm chung của ba đường phân giác trong của ΔDEF(Đpcm)