Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
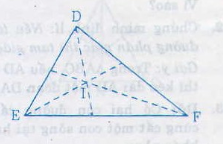
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc ˆDD^, ˆEE^, ˆFF^
Vậy I là điểm chung của ba đường phân giác của tam giác DEF

I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc ˆDD^, ˆEE^, ˆFF^
Vậy I là điểm chung của ba đường phân giác của tam giác DEF

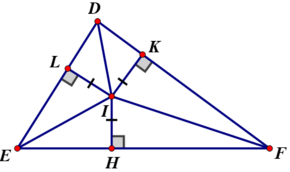
Gọi IH, IK, IL lần lượt là khoảng cách từ I đến EF, DF, DE.
Theo đề bài, điểm I cách đều ba cạnh của ΔDEF ⇒ IH = IK = IL
IL = IK ⇒ I cách đều hai cạnh của góc D ⇒ I nằm trên đường phân giác của góc D.
IH = IK ⇒ I cách đều hai cạnh của góc F ⇒ I nằm trên đường phân giác của góc F.
IH = IL ⇒ I cách đều hai cạnh của góc E ⇒ I nằm trên đường phân giác của góc E.
Từ 3 điều trên suy ra I là điểm chung của ba đường phân giác của tam giác DEF.

I D E F
I nằm trong ∆DEF và cách đều ba cạnh của tam giác nên I lần lượt thuộc phân giác của các góc ∠D, ∠E , ∠F
Vậy I là điểm chung của ba đường phân giác của tam giác DEF
mà hình như là đại học sư phạm rồi mà.bài dễ thế mà không biết làm à

Kẻ IA⊥ED tại A, IB⊥EF tại B, IC⊥DF tại C
Vì I cách đều ba cạnh nên IA=IB=IC
Xét ΔIAE vuông tại A và ΔIBE vuông tại B có
IE chung
IA=IB(cmt)
Do đó: ΔIAE=ΔIBE(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{AEI}=\widehat{BEI}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{DEI}=\widehat{FEI}\)
hay EI là tia phân giác của \(\widehat{DEF}\)(1)
Xét ΔICF vuông tại C và ΔIBF vuông tại B có
IF chung
IC=IB(cmt)
Do đó: ΔICF=ΔIBF(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BFI}=\widehat{CFI}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{EFI}=\widehat{DFI}\)
hay FI là tia phân giác của \(\widehat{EFD}\)(2)
Xét ΔDAI vuông tại A và ΔDCI vuông tại C có
DI chung
IA=IC(cmt)
Do đó: ΔDAI=ΔDCI(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ADI}=\widehat{CDI}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{EDI}=\widehat{FDI}\)
hay DI là tia phân giác của \(\widehat{EDF}\)(3)
Từ (1), (2) và (3) suy ra I là điểm chung của ba đường phân giác trong của ΔDEF(Đpcm)

Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng

Đe ma ban .vi G la trong tam nen AG la duong trung tuyen cua tam giac ABC ma tam giac ABC can nen dong thoi la duong phan giac.MATkhac I cach deu 3 canh nen ai la duong phan giac.dan den A,G,I thang hang