Giúp mình bài 4 với ạ mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=\dfrac{81}{4}+36=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\dfrac{81}{4}}{\dfrac{15}{2}}=\dfrac{27}{10}\)cm
=> \(CH=BC-BH=\dfrac{15}{2}-\dfrac{27}{10}=\dfrac{24}{5}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}\)
\(=\dfrac{4,5.6}{\dfrac{15}{2}}=\dfrac{18}{5}\)cm
tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=\left(4,5\right)^2+6^2=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}=7,5\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\left(4,5\right)^2}{7,5}=\dfrac{27}{10}=2,7\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{6^2}{7,5}=\dfrac{24}{5}=4,8\left(cm\right)\)

Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

b, lấy Uab=U=14V
K đóng \(=>\left(R1//R3\right)nt\left(R2//R4\right)\)
với chiều dòng điện từ D->C(qua ampe kế)
\(=>I=\dfrac{14}{Rtd}=\dfrac{14}{\dfrac{R1.R3}{R1+R3}+\dfrac{R2.R4}{R2+R4}}\)
\(=\dfrac{14}{\dfrac{2.3}{2+3}+\dfrac{2.4}{2+4}}=\dfrac{105}{19}A=I13=I24\)
\(=>U13=I13.R13=\dfrac{105}{19}.\dfrac{2.3}{2+3}=\dfrac{126}{19}V=U3\)
\(=>I3=\dfrac{126}{19}:3=\dfrac{42}{19}A\)
\(=>U24=I24.R24=\dfrac{105}{19}.\dfrac{2.4}{2+4}=\dfrac{140}{19}V=U4\)
\(=>I4=\dfrac{140}{19}:4=\dfrac{35}{19}A\)
\(=>I3=Ia+I4=>Ia=I3-I4=\dfrac{42}{19}-\dfrac{35}{19}=\dfrac{7}{19}A\)
K hở =>\(\left(R1ntR2\right)//\left(R3ntR4\right)\)(đề hơi khó nhìn )
\(=>Rtd=\dfrac{\left(R1+R2\right)\left(R3+R4\right)}{R1+R2+R3+R4}=\dfrac{\left(2+2\right)\left(3+4\right)}{2+2+3+4}=\dfrac{28}{11}\left(om\right)\)
\(=>I12+I34=\dfrac{U}{\dfrac{28}{11}}=\dfrac{11U}{28}\left(A\right)=>I34=\dfrac{11U}{28}-I12\)
giả sử chiều dòng điện qua vôn kế từ M->N
vôn kế chỉ \(1V=>\)\(-U1+U3=1\)
\(=>-I12.R1+I34.R3=1\)
\(=>-2.I12+3.I34=1\)
\(=>-2.I12+3\left(\dfrac{11U}{28}-I12\right)=1\)
\(=>-2.I12+\dfrac{33U}{28}-3I12=1\)
\(=>-5.I12+\dfrac{33U}{28}=1\)
\(=>-5.\dfrac{U}{2+2}+\dfrac{33U}{28}=1=>U=-14V\)
điều này chứng tỏ cực dương vôn kế mắc vào N, cực âm vôn kế mắc vào M thì U=14V
\(\)


\(B=2+2^2+2^3+2^4+...+2^{99}+2^{100}=2\left(1+2^2+2^3+2^4\right)+...+2^{96}\left(1+2^2+2^3+2^4\right)=2.31+2^6.31+...+2^{96}.31=31\left(2+2^6+...+2^{96}\right)⋮31\)
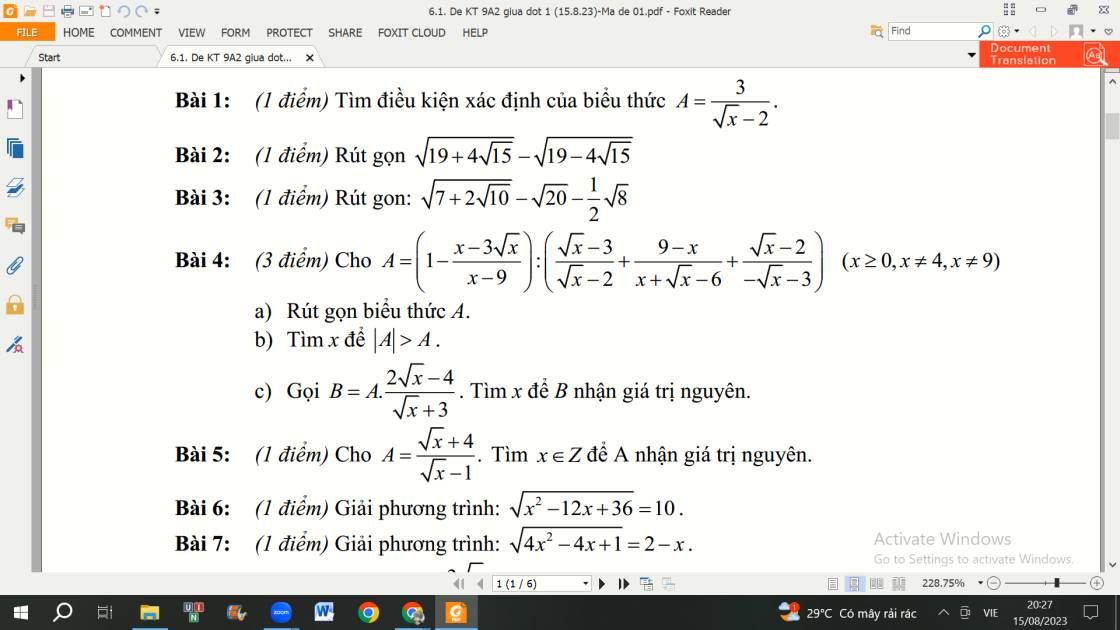


 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn

a.
\(SH\perp\left(ABC\right)\Rightarrow SH=d\left(S;\left(ABC\right)\right)\)
\(SH\perp\left(ABC\right)\Rightarrow SH\perp BC\Rightarrow\Delta SBH\) vuông tại H
\(BH=\dfrac{1}{2}BC=a\Rightarrow SH=\sqrt{SB^2-BH^2}=a\sqrt{3}\)
\(SH\perp\left(ABC\right)\Rightarrow HA\) là hình chiếu vuông góc của SA lên (ABC)
\(\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(AH=\dfrac{1}{2}BC=a\) (trung tuyến ứng với cạnh huyền)
\(\Rightarrow tan\widehat{SAH}=\dfrac{SH}{AH}=\sqrt{3}\Rightarrow\widehat{SAH}=60^0\)
b.
H là trung điểm BC, M là trung điểm AB \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH||AC\Rightarrow MH\perp AB\) (do \(AB\perp AC\))
Lại có \(SH\perp\left(ABC\right)\Rightarrow SH\perp AB\)
\(\Rightarrow AB\perp\left(SMH\right)\)
Mà \(AB=\left(SAB\right)\cap\left(ABC\right)\Rightarrow\widehat{SMH}\) là góc giữa (SAB) và (ABC)
\(AC=\sqrt{BC^2-AB^2}=a\sqrt{3}\) \(\Rightarrow MH=\dfrac{1}{2}AC=\dfrac{a\sqrt{3}}{2}\) (đường trung bình)
\(\Rightarrow tan\widehat{SMH}=\dfrac{SH}{MH}=2\Rightarrow\widehat{SMH}\approx63^023'\)
c.
Theo cmt: \(\left\{{}\begin{matrix}MH\perp SH\\MH\perp AB\end{matrix}\right.\) \(\Rightarrow MH\) là đường vuông góc chung của SH và AB
\(\Rightarrow d\left(SH;AB\right)=MH=\dfrac{a\sqrt{3}}{2}\)
Từ H kẻ HK vuông góc SM (K thuộc SM)
\(AB\perp\left(SMH\right)\Rightarrow AB\perp HK\)
\(\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
Hệ thức lượng trong tam giác vuông SMH:
\(HK=\dfrac{SH.MH}{\sqrt{SH^2+MH^2}}=\dfrac{a\sqrt{15}}{5}\)