giải phương trình ...
Đọc tiếp
giải phương trình : -36x4+97x2-36=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
27 tháng 1 2017
Đặt m = t 2 .Điều kiện m ≥ 0
Ta có: 36 t 4 – 13 t 2 +1 = 0 ⇔ 36 m 2 -13m +1 =0
Ta có: ∆ = - 13 2 – 4.36.1=169 -144=25 > 0
∆ = 25 = 5
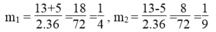
Ta có: t 2 =1/4 ⇒ t= ± 1/2
t 2 =1/9 ⇒ t= ± 1/3
Vậy phương trình đã cho có 4 nghiệm :
t 1 = 1/2 ; t 2 = -1/2 ; t 3 = 1/3 ; t 4 = -1/3
TN
24 tháng 5 2017
\(x^4+5x^2-36=0\)
\(\Leftrightarrow x^4-4x^2+9x^2-36=0\)
\(\Leftrightarrow x^2\left(x^2-4\right)+9\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x^2+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x^2+9\right)=0\)
Dễ thấy: \(x^2+9\ge9>0\forall x\) (vô nghiệm)
SUy ra \(x-2=0;x+2=0\Rightarrow x=2;x=-2\)
SY
24 tháng 5 2017
Đặt t = x2 ( t ≥ 0)
ta có phương trình: t2 + 5t – 36 = 0. Δt = 25 4.1.(-36) = 169
→ t1 = 4 (tmđk); t2 = -9 (loại). Với t = 4 → x2 = 4 → x = 2
KN
2 tháng 11 2019
\(2x^3+5x^2-36=0\)
\(\Leftrightarrow2x^3+9x^2-4x^2+18x-18x-36=0\)
\(\Leftrightarrow\left(2x^3+9x^2+18x\right)-\left(4x^2+18x+36\right)=0\)
\(\Leftrightarrow x\left(2x^2+9x+18\right)-2\left(2x^2+9x+18\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x^2+9x+18\right)=0\)
\(TH1:x-2=0\Leftrightarrow x=2\)
\(TH2:2x^2+9x+18=0\)
Ta có: \(\Delta=9^2-4.2.18=-63< 0\)
Vậy TH2 ko có nghiệm
Vậy x = 2
H
15 tháng 5 2023
`a,3x^2-3x(-2+x) <= 36`
`<=> 3x^2 + 6x -3x^2 <= 36`
`<=> 6x <= 36`
`<=> x <= 6`
Vậy bpt đã cho có tập nghiệm `x <= 6`
`b, (x+2)^2 -9>0`
`<=> (x+2)^2 > 9`
`<=>(x+2)^2 > 3^2`
`<=> x+2> +- 3`
`<=> x>1;-5`
Vậy bpt đã cho có tập nghiệm `x>1` hoặc `x> -5`
15 tháng 5 2023
a: =>3x^2+6x-3x^2<=36
=>6x<=36
=>x<=6
b: =>(x-1)(x+5)>0
=>x>1 hoặc x<-5
AH
Akai Haruma
Giáo viên
29 tháng 5 2023
Lời giải:
Lấy P(1) + 4PT(2) ta được:
$\sqrt{2x-y-9}+x^2-4xy+4y^2=0$
$\Leftrightarrow \sqrt{2x-y-9}+(2y-x)^2=0$
Do $\sqrt{2x-y-9}\geq 0; (2y-x)^2\geq 0$ với mọi $x,y$ tm điều kiện xác định nên để tổng của chúng bằng 0 thì:
$2x-y-9=2y-x=0$
$\Leftrightarrow 2x-y=9; x=2y$
$\Rightarrow x=18; y=9$
ND
2
Y
31 tháng 5 2023
\(a,3x^2-3x\left(-2+x\right)\le36\)
\(\Leftrightarrow3x^2+6x-3x^2-36\le0\)
\(\Leftrightarrow6x\le36\)
\(\Leftrightarrow x\le6\)
\(b,\left(x+2\right)^2-9>0\)
\(\Leftrightarrow\left(x+2\right)^2-3^2>0\)
\(\Leftrightarrow\left(x+2-3\right)\left(x+2+3\right)>0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1>0\\x+5>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>1\\x>-5\end{matrix}\right.\)
1 tháng 6 2023
b: =>(x+2-3)(x+2+3)>0
=>(x+5)(x-1)>0
=>x-1>0 hoặc x+5<0
=>x>1 hoặc x<-5
TT
6
29 tháng 4 2020
Bài làm
\(36^2+\frac{1}{x^2}+21x+\frac{7}{2x}-18=0\)
\(\Leftrightarrow\frac{36^2.2.x^2}{2x^2}+\frac{2}{2x^2}+\frac{2.x^2.21x}{2x^2}+\frac{7x}{2x^2}-\frac{2.x^2.18}{2x^2}=0\)
\(\Rightarrow2592x^2+2+42x^3+7x-36x^2=0\)
\(\Leftrightarrow2556x^2+42x^3+7x+2=0\)
tự giải nốt.
30 tháng 4 2020
Không có cách khác à bạn? Mình làm cách đấy rồi mà thấy nó dài vl luôn nên đăng nên hỏi coi có cách khác không
TT
1
CR
30 tháng 4 2020
pt trên \(< =>1296+\frac{2}{2x^2}+\frac{7x}{2x^2}+21x-18=0\)
\(< =>1278+\frac{7x+2}{2x}+21x=0\)
\(< =>1278+\frac{9}{2}=-21x\)
\(< =>\frac{2565}{2}=-21x\)
\(< =>x=\frac{2565}{-42}=-\frac{855}{14}\)
Ko chắc lắm :P
LN
2
17 tháng 4 2020
pt đã cho tương đương với (4x2-x+6)2=0
phần còn lại cậu tự giải đc
Đặt \(x^2=u\left(u\ge0\right)\), pt đã cho trở thành \(-36u^2+97u-36=0\) (*)
pt (*) có \(\Delta=97^2-4\left(-36\right)\left(-36\right)=4225>0\)
Nên pt này có 2 nghiệm phân biệt \(\left[{}\begin{matrix}u_1=\dfrac{-97+\sqrt{4225}}{2.\left(-36\right)}=\dfrac{4}{9}\left(nhận\right)\\u_2=\dfrac{-97-\sqrt{4225}}{2\left(-36\right)}=\dfrac{9}{4}\left(nhận\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2=\dfrac{4}{9}\\x^2=\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{2}{3}\\x=\pm\dfrac{3}{2}\end{matrix}\right.\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\pm\dfrac{2}{3};\pm\dfrac{3}{2}\right\}\)