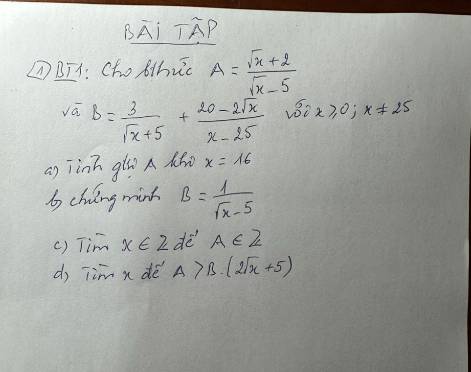Giải giúp mình câu b và c với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H
HT2k02
6 tháng 4 2021
Đúng(1)
Những câu hỏi liên quan
giải giúp mình câu b, c với ạ!
VV
3
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
b.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x-\dfrac{1}{2}sin2x=-cosx\)
\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{6}\right)=cos\left(x+\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{6}=x+\pi+k2\pi\\2x+\dfrac{\pi}{6}=-x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{6}+k2\pi\\x=-\dfrac{7\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
c.
\(\Leftrightarrow2cos4x.sin3x=2sin4x.cos4x\)
\(\Leftrightarrow cos4x\left(sin4x-sin3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\sin4x=sin3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\pi}{2}+k\pi\\4x=3x+k2\pi\\4x=\pi-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=k2\pi\\x=\dfrac{\pi}{7}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
2.
\(f\left(x\right)=\dfrac{1}{2}-\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x-5\)
\(=-\dfrac{9}{2}-\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)\)
\(=-\dfrac{9}{2}-cos\left(2x-\dfrac{\pi}{3}\right)\)
Do \(-1\le-cos\left(2x-\dfrac{\pi}{3}\right)\le1\Rightarrow-\dfrac{11}{2}\le y\le-\dfrac{7}{2}\)
\(y_{min}=-\dfrac{11}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
\(y_{max}=-\dfrac{7}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\Rightarrow x=\dfrac{2\pi}{3}+k\pi\)
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
AH
0
VV
0
DN
2
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
12.
\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)
\(\Rightarrow M=\sqrt{2}\)
13.
Pt có nghiệm khi:
\(5^2+m^2\ge\left(m+1\right)^2\)
\(\Leftrightarrow2m\le24\)
\(\Rightarrow m\le12\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
14.
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x=k2\pi\)
15.
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)
Đáp án A
16.
\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)
Có \(1008+1008=2016\) nghiệm
U
1
8 tháng 6 2021
Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....
18 tháng 9 2023
a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)