Tính diện tích hình thang cân, biết hai cạnh đáy là 12cm và 18cm, góc ở đáy bằng 75 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,góc D = 75 °
Kẻ AH ⊥ CD, BK ⊥ CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: ∆ ADH = ∆ BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK


gọi hình thang cân là ABCD,AB=8,DC=12
kẻ AH vuông gócvới DC,BK vgóc với DC
=> AB=HK=8.Vì đây là hình thang cân nên DH=KC mà DC=12=>DH=(12-8)/2=2.
Mà góc ở đáy bằng 75 độ rồi áp dụng hệ thức lượng vào tam giác vuông ADH=> AH=...Rồi áp dụng công thức tính S hình thang:Đáy lớn +đáy bé nhân chiều cao chia hai
0

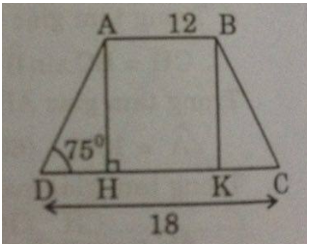
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,
Kẻ
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Chúc bạn học tốt , bạn nhớ cho mình 1 like nhé !
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
Trong tam giác vuông ADH, ta có:
Vậy:
(cm2).
Tham khảo:

Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,\(\widehat{D}\)\(=75^0\)
Kẻ AH ⊥ CD, BK ⊥ CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra: \(DH=\dfrac{CD-HK}{2}=\dfrac{18-12}{2}=3\) ( cm )
Trong tam giác vuông ADH, ta có:
\(AH=DH.tgD=3.tg75^0\approx11,196\) ( cm )
Vậy: \(S_{ABCD}=\dfrac{AB+CD}{2}.AH=\dfrac{12+18}{2}.11,196=167,94\) ( cm\(^2\) )

Bài làm:
Tổng độ dài hai đáy là
10.2=20(cm)
Độ dài đáy AB là
20-12=8(cm)
Chiều cao của hình thang là
8-3=5(cm)
Diện tích hình thang cân ABCD là
(12+8).5:2 =50(cm2)
Dấu . là nhân nha!!
cm2 là cm vuông!!

Lời giải:
Kẻ $AH\perp DC$.
Do $ABCD$ là htc nên $DH=(DC-AB):2=(20-15):2=2,5$ (cm)
Xét tam giác vuông $ADH$ có:
$\frac{AH}{DH}=\tan D=\tan 75^0$
$\Rightarrow AH=DH\tan 75^0=2,5\tan 75^0=9,33$ (cm)
$S_{ABCD}=(AB+CD).AH:2=(15+20).9,33:2=163,275$ (cm2)


Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, ˆD=75∘D^=75∘
Kẻ AH⊥CD,BK⊥CDAH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=
111,9615242cm2