NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
20 tháng 12 2019
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,góc D = 75 °
Kẻ AH ⊥ CD, BK ⊥ CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: ∆ ADH = ∆ BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
NT
1
HV
22 tháng 10 2016
gọi hình thang cân là ABCD,AB=8,DC=12
kẻ AH vuông gócvới DC,BK vgóc với DC
=> AB=HK=8.Vì đây là hình thang cân nên DH=KC mà DC=12=>DH=(12-8)/2=2.
Mà góc ở đáy bằng 75 độ rồi áp dụng hệ thức lượng vào tam giác vuông ADH=> AH=...Rồi áp dụng công thức tính S hình thang:Đáy lớn +đáy bé nhân chiều cao chia hai
0
18 tháng 8 2021
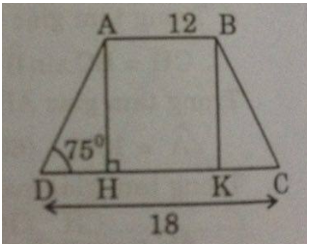
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,
Kẻ
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Chúc bạn học tốt , bạn nhớ cho mình 1 like nhé !
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
Trong tam giác vuông ADH, ta có:
Vậy:
(cm2).
18 tháng 8 2021
Tham khảo:
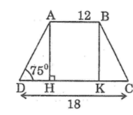
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,\(\widehat{D}\)\(=75^0\)
Kẻ AH ⊥ CD, BK ⊥ CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra: \(DH=\dfrac{CD-HK}{2}=\dfrac{18-12}{2}=3\) ( cm )
Trong tam giác vuông ADH, ta có:
\(AH=DH.tgD=3.tg75^0\approx11,196\) ( cm )
Vậy: \(S_{ABCD}=\dfrac{AB+CD}{2}.AH=\dfrac{12+18}{2}.11,196=167,94\) ( cm\(^2\) )
YN
0
AH
Akai Haruma
Giáo viên
27 tháng 5 2023
Lời giải:
Kẻ $AH\perp DC$.
Do $ABCD$ là htc nên $DH=(DC-AB):2=(20-15):2=2,5$ (cm)
Xét tam giác vuông $ADH$ có:
$\frac{AH}{DH}=\tan D=\tan 75^0$
$\Rightarrow AH=DH\tan 75^0=2,5\tan 75^0=9,33$ (cm)
$S_{ABCD}=(AB+CD).AH:2=(15+20).9,33:2=163,275$ (cm2)
1 tháng 9 2020
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, D^=75∘
Kẻ AH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=167,94 (cm2).
111,9615242cm2