Giúp mình các pt với ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0\) ; \(\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m+1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(x_1+x_2\right)=-2m+1\\4x_1x_2=2m-2\end{matrix}\right.\)
Cộng vế với vế:
\(\Rightarrow2\left(x_1+x_2\right)+4x_1x_2=-1\)
Đây là hệ thức liên hệ các nghiệm ko phụ thuộc m

=>(50x+50x+250+65x+11050)*1,1=216500
=>165x+11300=196818,1818
=>165x=185518,1818
=>\(x\simeq124.353\)

\(\left(x^2+1\right)\left(x-\frac{1}{2}\right)=0\)
Vì x2 > 0 => x2+1 >0
=> \(x-\frac{1}{2}=0\)
=> \(x=\frac{1}{2}\)
\(\Leftrightarrow x^2-3x+2=0\)
\(\Leftrightarrow x^2-x-2x-2=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=1\end{cases}}}\)
*) \(x^2-2=3x-4\)
*) x2-2=3x-4
<=> x2-2-3x+4=0
<=> x2-3x+2=0
<=> x2-x-2x+2=0
<=> x(x-1)-2(x-1)=0
<=> (x-1)(x-2)=0
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=2\end{cases}}}\)

\(\text{Δ}=\left(2m-1\right)^2-8\left(m-1\right)\)
\(=4m^2-4m+1-8m+8\)
\(=4m^2-12m+9=\left(2m-3\right)^2\)
Để phương trình có hai nghiệm phân biệt thì 2m-3<>0
hay m<>3/2
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x_1-4x_2=11\\x_1+x_2=\dfrac{-2m+1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_1-4x_2=11\\2x_1+2x_2=-2m+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x_1-4x_2=11\\4x_1+4x_2=-4m+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x_1=-4m+13\\4x_2=3x_1-11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-4m+13}{7}\\4x_2=\dfrac{-12m+36}{7}-\dfrac{77}{7}=\dfrac{-12m-41}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-4m+13}{7}\\x_2=\dfrac{-12m-41}{28}\end{matrix}\right.\)
Theo Vi-et, ta được: \(x_1x_2=\dfrac{m-1}{2}\)
\(\Leftrightarrow\dfrac{\left(4m-13\right)\left(12m+41\right)}{196}=\dfrac{m-1}{2}\)
\(\Leftrightarrow\left(4m-13\right)\left(12m+1\right)=98\left(m-1\right)\)
\(\Leftrightarrow48m^2+4m-156m-13-98m+98=0\)
\(\Leftrightarrow48m^2-250+85=0\)
Đến đây bạn chỉ cần giải pt bậc hai là xong rồi
\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+10\)
\(=\left(2m-3\right)^2+1>0\)
Vậy pt có 2 nghiệm pb
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1-2m}{2}\left(1\right)\\x_1x_2=\dfrac{m-1}{2}\left(2\right)\end{matrix}\right.\)
Ta có \(3x_1-4x_2=11\left(3\right)\)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}4x_1+4x_2=2-4m\\3x_1-4x_2=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x_1=13-4m\\x_2=\dfrac{1-2m}{2}-x_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{13-4m}{7}\\x_2=\dfrac{1-2m}{2}-\dfrac{13-4m}{7}\end{matrix}\right.\)
\(x_2=\dfrac{7-14m-26+8m}{14}=\dfrac{-19-6m}{14}\)
Thay vào (2) ta được \(\left(\dfrac{13-4m}{7}\right)\left(\dfrac{-19-6m}{14}\right)=\dfrac{m-1}{2}\)
\(\Leftrightarrow m=4,125\)


\(\sqrt{4x^2-4x+9}=3\)
\(\Leftrightarrow4x^2-4x+9=9\Leftrightarrow4x^2-4x=0\)
\(\Leftrightarrow4x\left(x-1\right)=0\Leftrightarrow x=0;1\)
\(\sqrt{4x^2-4x+9}=3\)
\(\Leftrightarrow\left(\sqrt{4x^2-4x+9}\right)^2=3^2\)
\(\Leftrightarrow4x^2-4x+9=9\)
\(\Leftrightarrow4x^2-4x=0\)\(\Leftrightarrow4x\left(x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}4x=0\\x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\)
Vậy tập nghiệm của pt là S={0;1}
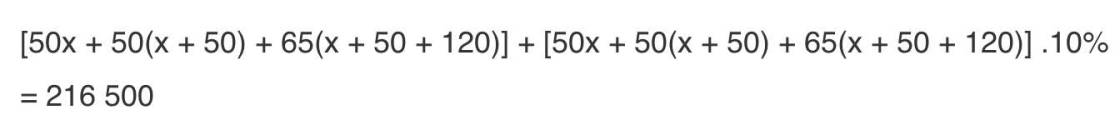
 các bạn ơi giúp mình với ạ!!! mình cần gấp lắm ạ. mong các bạn giúp mình. cảm ơn ạ
các bạn ơi giúp mình với ạ!!! mình cần gấp lắm ạ. mong các bạn giúp mình. cảm ơn ạ
\(a,Cl_2+2NaOH\rightarrow NaCl+NaClO+H_2O\\ b,Br_2+2NaI\rightarrow2NaBr+I_2\uparrow\\ c,H_2S+4Cl_2+H_2O\rightarrow H_2SO_4+8HCl\uparrow\)
\(d,SO_2+Br_2+2H_2O\rightarrow H_2SO_4+2HBr\uparrow\\ d,2KI+O_3+H_2O\rightarrow I_2\uparrow+2KOH+O_2\uparrow\\ e,2F_2+2H_2O_{\left(băng\right)}\underrightarrow{< 0^oC}4HF+O_2\\ f,2H_2S+3O_{2\left(dư\right)}\underrightarrow{t^o}2H_2O+2SO_2\uparrow\)
\(g,Al_2S_3+6HCl\rightarrow2AlCl_3+3H_2S\uparrow\\ h,2KMnO_4+16HCl\rightarrow2KCl+2MnCl_2+5Cl_2\uparrow+8H_2O\\ i,2Fe+6H_2SO_{4\left(đ,n\right)}\rightarrow Fe_2\left(SO_4\right)_3+3SO_2\uparrow+6H_2O\\ k,2P+5H_2SO_{4\left(đ,n\right)}\rightarrow2H_3PO_4+2H_2O+5SO_2\uparrow\)