Cho hình chóp S.ABC, có \(\widehat{ASB\: =}90^0,\widehat{BSC}=60^0,\widehat{CSA}=120^0,SC=a\sqrt{2}.\) Tính khoảng cách từ C đến (SAB).
A. \(\dfrac{a}{4}\)
B. a
C. \(\dfrac{a}{2}\)
D. \(\dfrac{3a}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(V=\dfrac{a.a\sqrt{3}.a\sqrt{2}}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290-cos^260-cos^2120}=\dfrac{a^3\sqrt{3}}{6}\)
5 tháng 4 2016
Dùng định lý hàm số Cosin tính được \(MN=2a\sqrt{3}\)
\(AM=2a\sqrt{2},AN=2a\). Tam giác vuông SAC có SC=2SA nên góc ASC =60 độ suy ra tam giác AMN vuông tại A.
Gọi H là trung điểm của MN, vì SA=SM=SN và tam giác AMN vuông tại A \(\Rightarrow SH\perp\left(AMN\right)\), tính được SH=a
Tính được \(V_{S.AMN}=\frac{2\sqrt{2}a^3}{3}\)
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SM.SN}{SB.SC}=\frac{1}{3}\) \(\Rightarrow V_{S.ABC}=2\sqrt{2}a^3\)
Vậy d(C;(SAB)) =\(\frac{3V_{S.ABC}}{S_{\Delta SAB}}=\frac{6a^3\sqrt{2}}{3a^2}=2a\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)
\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 2 2021
\(AB=\sqrt{SA^2+SB^2}=a\sqrt{2}\)
\(AC=\sqrt{SA^2+SC^2-2SA.SC.cos120^0}=\sqrt{3}\)
\(BC=\sqrt{SB^2+SC^2-2SB.SC.cos60^0}=a\)
\(\Rightarrow AB^2+BC^2=AC^2\Rightarrow\Delta ABC\) vuông tại B
Gọi H là hình chiếu vuông góc của S lên (ABC) \(\Rightarrow\) H là tâm đường tròn ngoại tiếp ABC (do SA=SB=SC)
\(\Rightarrow\) H trùng trung điểm AC
Gọi M là trung điểm SA \(\Rightarrow MH||SC\Rightarrow\) góc giữa SC và (SAB) bằng góc giữa MH và (SAB)
Gọi N là trung điểm AB \(\Rightarrow HN\perp AB\Rightarrow AB\perp\left(SHN\right)\)
Trong mp (SHN), kẻ \(HK\perp SN\Rightarrow HK\perp\left(SAB\right)\)
\(\Rightarrow\widehat{KMH}\) là góc giữa SC và (SAB)
\(SH=\sqrt{SA^2-\left(\dfrac{AC}{2}\right)^2}=...\)
\(MH=\dfrac{1}{2}SA=...\) (trung tuyến ứng với cạnh huyền)
\(NH=\dfrac{1}{2}BC=...\) (đường trung bình)
\(\Rightarrow\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{NH^2}\Rightarrow HK=...\)
\(\Rightarrow sin\widehat{KMH}=\dfrac{HK}{MH}=...\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
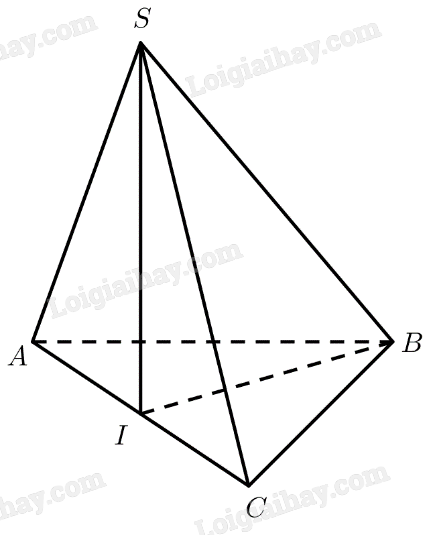
Xét tam giác \(SAC\) có:
\(AC = \sqrt {S{A^2} + S{C^2} - 2.SA.SC.\cos \widehat {ASC}} = a\sqrt 3 \)
\(SI\) là trung tuyến \( \Rightarrow SI = \frac{{\sqrt {2\left( {S{A^2} + S{C^2}} \right) - A{C^2}} }}{2} = \frac{a}{2}\)
Ta có: \(S{I^2} + A{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{A^2}\)
\( \Rightarrow \Delta SAI\) vuông tại \(I \Rightarrow SI \bot AC\)
Xét tam giác \(SAB\) vuông tại \(S\) có: \(AB = \sqrt {S{A^2} + S{B^2}} = a\sqrt 2 \)
Xét tam giác \(SBC\) cân tại \(S\) có \(\widehat {BSC} = {60^ \circ }\) nên tam giác \(SBC\) đều. Vậy \(BC = a\)
Xét tam giác \(ABC\) có: \(A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2} = A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(B \Rightarrow BI = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(SBI\) có: \(S{I^2} + B{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{B^2}\)
\( \Rightarrow \Delta SBI\) vuông tại \(I \Rightarrow SI \bot BI\)
Ta có:
\(\left. \begin{array}{l}SI \bot AC\\SI \bot BI\end{array} \right\} \Rightarrow SI \bot \left( {ABC} \right)\)
CM
31 tháng 3 2019
Đáp án D
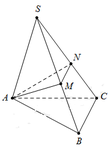
Gọi M, N lần lượt thuộc cạnh SB,SC sao cho S M = S N = 2.
Tam giác SMN đều ⇒ S M = S N = M N = 2.
Tam giác SAM có AS M ^ = 45 ∘ ⇒ A M = 2 2 − 2 .
Tam giác SAN vuông cân tại S ⇒ A N = S A 2 = 2 2 .
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ⇒ S I ⊥ A M N .
Tính bán kính đường tròn ngoại tiếp Δ A M N . Diện tích tam giác AMN là
S = p p − A M p − A N p − M N ⇒ R Δ A M N = A M . A N . M N 4 S = 2 4 − 2 2 S Δ A M N ,
với p = A M + A N + M N 2 .
Tam giác SAI vuông tại I, có S I = S A 2 − I A 2 = 4 − R 2 Δ A M N .
Ta có V S . A M N V S . A B C = S M S B . S N S C = 2 3 . 2 4 = 1 3 ⇒ V S . A B C = 3 V S . A M N ⇒ d B ; S A C = 9 V S . A M N S Δ S A C = 3 2 .
Đặt \(SA=x;SB=y\)
\(S_{\Delta SAB}=\dfrac{1}{2}SA.SB=\dfrac{xy}{2}\)
\(V=\dfrac{SA.SB.SC}{6}.\sqrt{1+2.cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{axy}{6}\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=\dfrac{3V}{S}=\dfrac{axy}{2.\dfrac{xy}{2}}=a\)