Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(V=\dfrac{a.a\sqrt{3}.a\sqrt{2}}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290-cos^260-cos^2120}=\dfrac{a^3\sqrt{3}}{6}\)

(h.3.19)
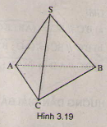
= SA.SC.cos - SA.SB.cos
= 0.
Vậy SA ⊥ BC.
\(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}\left(\overrightarrow{SC}-\overrightarrow{SA}\right)=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\)
\(=SB.SC.cos\widehat{BSC}-SB.SA.cos\widehat{BSA}=0\).
Vậy \(SB\perp AC\).
\(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.\left(\overrightarrow{SB}-\overrightarrow{SA}\right)=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA}\)
\(=SC.SB.cos\widehat{BSC}-SC.SA.cos\widehat{CSA}=0\).
Vậy \(SC\perp AB\).

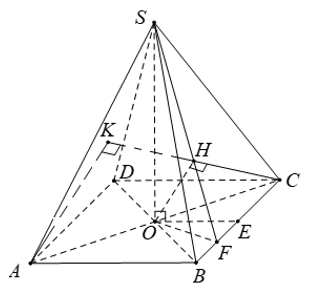
S A B C D O H
Do \(\left\{{}\begin{matrix}SA=SC\\SB=SD\end{matrix}\right.\) \(\Rightarrow\) hình chiếu vuông góc của S lên đáy trùng tâm đáy
\(\widehat{BAD}=60^0\Rightarrow\Delta BAD\) đều \(\Rightarrow BD=a\Rightarrow OB=\frac{a}{2}\)
\(\Rightarrow SO=\sqrt{SB^2-OB^2}=\frac{a\sqrt{11}}{2}\)
b/ Kẻ \(OH\perp AB\Rightarrow AB\perp\left(SOH\right)\Rightarrow\widehat{SHO}\) là góc giữa (SAB) và (ABCD)
\(OH=\frac{1}{2}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}\Rightarrow tan\varphi=\frac{SO}{OH}=\frac{2\sqrt{33}}{3}\)

Bạn coi lại dữ liệu bài toán, vừa thừa vừa thiếu
SA=SC=AC nên tam giác SAC đều thì hiển nhiên \(\widehat{CSA}=60^0\) ko cần đề bài phải cho nữa
\(\widehat{ASB}=90^0\) và SA=SB thì tam giác SAB vuông cân tại S nên ta có \(AB=\sqrt{SA^2+SB^2}=a\sqrt{2}\) cũng không cần đề phải cho
Nhưng hoàn toàn ko có dữ liệu BC hoặc góc A của tam giác ABC để định dạng đáy



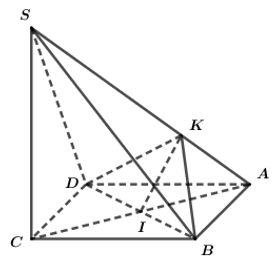




Đặt \(SA=x;SB=y\)
\(S_{\Delta SAB}=\dfrac{1}{2}SA.SB=\dfrac{xy}{2}\)
\(V=\dfrac{SA.SB.SC}{6}.\sqrt{1+2.cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{axy}{6}\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=\dfrac{3V}{S}=\dfrac{axy}{2.\dfrac{xy}{2}}=a\)