cho nửa đường tròn o bán kính r đường kính AB, B thuộc nửa đường tròn. trên dây BM lấy N, tia AN cắt nửa đường (o) tại P, tia AM cắt PB tại Q
a)CM 4 điểm M,N,P,Q thuộc 1 đường tròn
b) CM tg MAB đồng dạng tg MNQ
c)MO là tiếp tuyến của đường tròn ngoại tiếp tg MNQ
d) dựng hbh ANBC, CM QB=QC.sinQPM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 12 2016
(\(M\) là giao của phân giác \(\widehat{BAC}\) và \(OC\) phải không bạn? À chắc chắn là vậy rồi.)
Câu a: Chính là hệ thức lượng trong tam giác vuông \(BPA\) đường cao \(BQ\).
Câu b: CM được tam giác \(AOC\) đều (3 cạnh bằng nhau) nên phân giác \(AM\) cũng là đường cao.
Vậy \(PM⊥MO\) mà lại có \(PB⊥BO\) nên \(B,P,M,O\) cùng thuộc đường tròn đường kính \(PO\).
Câu c: \(\frac{PB}{KB}=\frac{PB}{AB}.\frac{AB}{KB}=\tan\widehat{PAB}.\cot\widehat{KAB}=\frac{1}{3}\) và ta có đpcm.
20 tháng 1
a: Sửa đề: OE\(\perp\)AN
Xét tứ giác OBME có \(\widehat{OBM}+\widehat{OEM}=90^0+90^0=180^0\)
=>OBME là tứ giác nội tiếp
=>O,B,M,E cùng thuộc một đường tròn
b: Ta có: ΔOAN cân tại O
mà OE là đường cao
nên OE là phân giác của góc AON
=>OK là phân giác của góc AON
Xét ΔONK và ΔOAK có
ON=OA
\(\widehat{NOK}=\widehat{AOK}\)
OK chung
Do đó: ΔONK=ΔOAK
=>\(\widehat{OAK}=\widehat{ONK}\)
mà \(\widehat{ONK}=90^0\)
nên \(\widehat{OAK}=90^0\)
=>KA là tiếp tuyến của (O)
NC
29 tháng 3 2016
a) Góc EBH = góc HBA ( góc nội tiếp chắn hai cung bằng nhau)
BH vuông góc EA ( góc AHB =90 nội tiếp chắn nửa đường tròn )
=> Có đpcm
b) KH.KB= KE ^2 ( dùng htl tỏng tam giác BAK )
26 tháng 5 2021
b) Dễ thấy C là trực tâm của tam giác IAB nên C, I, H thẳng hàng.
Do tứ giác AICK là hình thang nội tiếp được đường tròn nên là hình thang cân.
Khi đó \(\widehat{IAK}=\widehat{CKA}\Rightarrow\widehat{IAB}=\widehat{NBA}\)
Suy ra tam giác NAB vuông cân tại N nên \(\widehat{NBA}=45^o\).
Ta có các tứ giác CMIN, AMIH nội tiếp được nên \(\widehat{NMH}=\widehat{NMI}+\widehat{HMI}=\widehat{ICN}+\widehat{IAB}=45^o+45^o=90^o\Rightarrow MN\perp MH\).
26 tháng 5 2021
c) Đề phải là \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}\ge6\).
Đặt \(x=\dfrac{IH}{CH};y=\dfrac{IN}{AN};z=\dfrac{IM}{BM}\left(x,y,z< 1\right)\).
Ta có \(x+y+z=\dfrac{S_{IAB}}{S_{ABC}}+\dfrac{S_{IBC}}{S_{ABC}}+\dfrac{S_{ICA}}{S_{ABC}}=1\).
Lại có \(\dfrac{IH}{CH}=x\Rightarrow\dfrac{CH}{IH}=\dfrac{1}{x}\Rightarrow\dfrac{IC}{IH}=\dfrac{1}{x}-1\).
Tương tự \(\dfrac{IA}{IN}=\dfrac{1}{y}-1;\dfrac{IB}{IM}=\dfrac{1}{z}-1\).
Do đó \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-3\ge_{Svacxo}\dfrac{9}{x+y+z}-3=\dfrac{9}{1}-3=6\).
Vậy ta có đpcm.
13 tháng 3 2015
ban tu ve hinh nhe
Ta co goc AEBnam ngoai dt nen goc AEB = 1/2(CUNG AB-cungHM)=1/2(cungHM+ cung MB)
ma goc Achan cung HB nen AEB=A nen tam giac AEB can o B
ban se de cm duoc AEBK thuoc 1dt nenKEB=90 nen KE^2=KH.KB
xet tam giac AEB co EI la duong cao con lai nenEIM dong dang EAB nenEIM=EBA
ma EBA=MBN nen EIM=MBN
ma EIM VA MBNcung nhin EN nenIENB thuoc 1duong tron
DT
17 tháng 2 2021
Xét ΔABC có AB là đườn kính đường tròn ngoại tiếp tam giác
=> ΔABC vuông tại C hay AP ⊥ BC
CMTT => AN ⊥ BP
Xét tứ giác PCMN có: \(\widehat{PCM}+\widehat{PNM}=90^o+90^o=180^o\)
=> PCMN là tứ giác nội tiếp
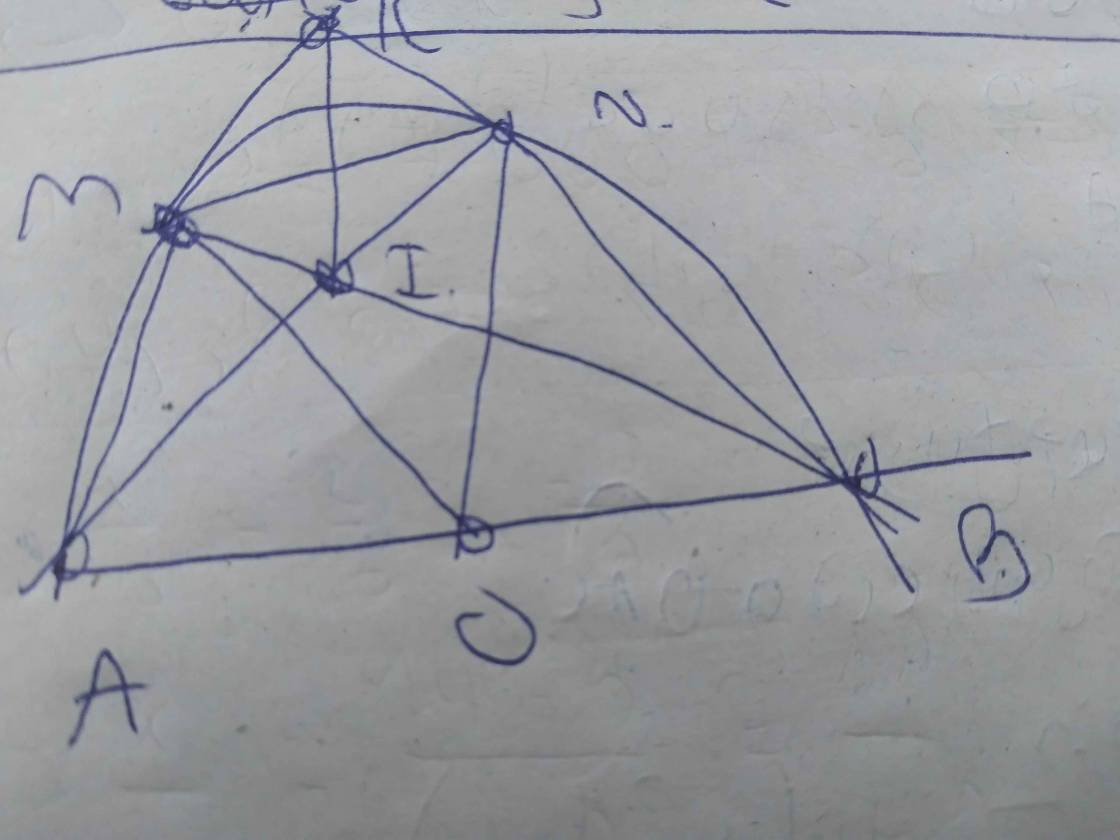
a: góc AMB=góc APB=1/2*sđ cung AB=90 độ
góc QMN+góc QPN=180 độ
=>QMNP là tứ giác nội tiếp
b: Xét ΔQBA có
AP,BM là đường cao
AP cắt BM tại N
=>N là trực tâm
=>QN vuông góc AB tại E
Xét ΔMAB vuông tại A và ΔMNQ vuông tại M có
góc MAB=góc MNQ(=góc ENB)
=>ΔMAB đồng dạng với ΔMNQ
c: Gọi F là trung điểm của QN
=>F là tâm đường tròn ngoại tiếp ΔMNQ
góc FMO=góc FMN+góc OMN
=góc FNM+góc OBN
=góc OBN+góc ENB=90 độ
=>MO là tiếp tuyến của đường tròn ngoại tiếp ΔMNQ