Cho \(\Delta ABC\)cân tại A . Trên cạnh đáy BC lấy D sao cho 2BD=CD . cmr góc BAD<\(\frac{1}{2}\)góc CAD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
14 tháng 3 2018
Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Lê Tự Nhật Thạch - Toán lớp 7 - Học toán với OnlineMath
CH
Cô Hoàng Huyền
Admin
VIP
14 tháng 3 2018
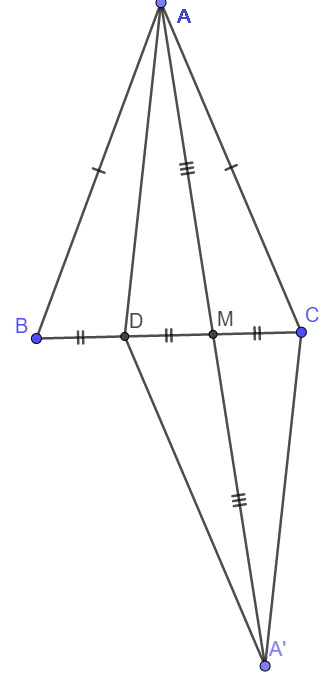
Gọi M là trung điểm DC và A' là điểm thuộc tia AM sao cho AM = MA'.
Khi đó ta thấy ngay \(\Delta AMC=\Delta A'MD\left(c-g-c\right)\)
\(\Rightarrow\widehat{MAC}=\widehat{MA'D}\) và AC = A'D.
Ta cũng có ngay \(\Delta ABD=\Delta ACM\left(c-g-c\right)\Rightarrow\widehat{BAD}=\widehat{CAM}\) và AB = AC
Kẻ AH vuông góc BC. Do tam giác ABC cân nên AH đồng thời là trung tuyến.
Vậy thì ta thấy ngay DH < BH nên theo quan hệ giữa đường xiên và hình chiếu ta có AD < AB
Suy ra AD < AC hay AD < DA'
Xét tam giác ADA' có AD < DA' nên theo quan hệ giữa cạnh và góc trong tam giác ta có :
\(\widehat{DAM}>\widehat{DA'M}\Rightarrow\widehat{DAM}>\widehat{MAC}\)
Lại có \(\widehat{DAM}+\widehat{MAC}=\widehat{CAD}\) nên \(\widehat{MAC}< \frac{1}{2}\widehat{CAD}\)
Vậy thì \(\widehat{BAD}< \frac{1}{2}\widehat{CAD}\left(đpcm\right)\)
NT
Cho tam giác ABC cân. Trên cạnh đáy BC lấy điểm D sao cho CD = 2BD. So sánh số đo hai góc BAC và CAD
1
CH
Cô Hoàng Huyền
Admin
VIP
14 tháng 3 2018
Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Lê Tự Nhật Thạch - Toán lớp 7 - Học toán với OnlineMath
1 tháng 2 2018
tam giác cân thì tận dụng đường cao, vẽ đường cao AH, H thuộc BC, H là trung điểm BC, dễ dàng tính được HC= 3/4 DC = 3a/2
AH chia góc BAC thành hai góc nhỏ gọi là A1 và A2, hai góc bằng nhau bằng 1/2 BAc= 60 độ, có HC có góc HAC thì tính được cạnh AH, ta tính được cạnh DH có AH nên tính được góc ADC, DAH, .... tính được các góc tam giác ADC, mà ban đầu thì bạn có thể tính ngay góc ACD rồi, tam giác cân mà, nói chung có nhiều cách làm lắm, muốn tính như nào cũng được, cơ bản thì bạn phải kẻ đường cao
R
0
22 tháng 2 2022
Bài 1:
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB>AC
nên BD>CD
20 tháng 2 2022
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Xét ΔKBD và ΔKCE có
\(\widehat{KBD}=\widehat{KCE}\)
BD=CE
\(\widehat{KDB}=\widehat{KEC}\)
Do đó:ΔKBD=ΔKCE
30 tháng 3 2021
a) Xét ΔBED và ΔBAD có
BE=BA(gt)
\(\widehat{EBD}=\widehat{ABD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔBED=ΔBAD(c-g-c)