Ai giải giúp mình với. X^2+4x-4y^2+8y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 10 2021
a, TK: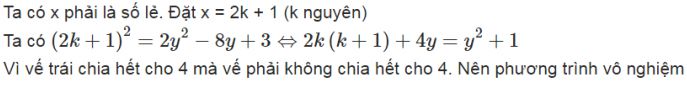
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương
PA
2
HP
3 tháng 10 2021
a. 3x2 - 4y2 = 18
<=> \(\left\{{}\begin{matrix}3x^2=18+4y^2\\4y^2=-\left(3x^2-18\right)\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{\dfrac{18+4y^2}{3}}\\y=\sqrt{\dfrac{-3x^2+18}{4}}\end{matrix}\right.\)
b, c, d tương tự nhé
HP
3 tháng 10 2021
b. 19x2 + 28y2 = 2001
<=> \(\left\{{}\begin{matrix}19x^2=2001-28y^2\\28y^2=2001-19x^2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{\dfrac{2001-28y^2}{19}}\\y=\sqrt{\dfrac{2001-19x^2}{28}}\end{matrix}\right.\)
c. x2 = 2y2 - 8y + 3
<=> \(\left\{{}\begin{matrix}x=\sqrt{2y^2-8y+3}\\8y=2y^2+3-x^2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{2y^2-8y+3}\\y=\dfrac{2y^2+3-x^2}{8}\end{matrix}\right.\)
d. x2 + y2 - 4x + 4y = 1
<=> \(\left\{{}\begin{matrix}x^2=1-y^2+4x-4y\\y^2=1-x^2+4x-4y\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{1-y^2+4x-4y}\\y=\sqrt{1-x^2+4x-4y}\end{matrix}\right.\)
TH
0
31 tháng 8 2019
Ta có: A = 4x2 + y2 + 4x - 4y - 3 = (4x2 + 4x + 1) + (y2 - 4y + 4) - 10 = (2x + 1)2 + (y - 2)2 - 10
Ta luôn có: (2x + 1)2 \(\ge\)0 \(\forall\)x
(y - 2)2 \(\ge\)0 \(\forall\)y
=> (2x + 1)2 + (y - 2)2 - 10 \(\ge\) -10 \(\forall\)x;y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}2x+1=0\\y-2=0\end{cases}}\) <=> \(\hept{\begin{cases}x=-\frac{1}{2}\\y=2\end{cases}}\)
Vậy MinA = -10 <=> x = -1/2 và y = 2
B = x2 + 4y2 - 4x + 4y + 3 = (x2 - 4x + 4) + (4y2 + 4y + 1) - 2 = (x - 2)2 + (2y + 1)2 - 2
còn lại tương tự
3 tháng 10 2021
d) \(x^2+y^2-4x+4y=1\\ \Rightarrow\left(x-2\right)^2+\left(y+2\right)^2=8\)
\(\Rightarrow8=\left(x-2\right)^2+\left(y+2\right)^2\ge\left(x-2\right)^2\)
\(\Rightarrow\left(x-2\right)^2\le8\)
Mà \(\left(x-2\right)^2\) là SCP và là số chẵn nên \(\left(x-2\right)^2\in\left\{0;4\right\}\)
Th1: \(\left(x-2\right)^2=0\Rightarrow\left(y+2\right)^2=8\left(vôlí\right)\)
Th2: \(\left(x-2\right)^2=4\Rightarrow\left(y+2\right)^2=4\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2=-2\\y+2=-2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=-2\\y+2=2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=2\\y+2=-2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=2\\y+2=2\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=0\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(0;-4\right);\left(0;0\right);\left(4;-4\right);\left(4;0\right)\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 10 2020
Bạn không nêu yêu cầu đề bài thì ai biết mà giúp bạn đúng ko?
R
4
6 tháng 6 2019
\(x^2+4y^2-4x-4y+5=0\)
\(\Leftrightarrow x^2-4x+4+4y^2-4y+1=0\)
\(\Leftrightarrow\left(x^2-2\cdot x\cdot2+2^2\right)+\left[\left(2y\right)^2-2\cdot2y\cdot1+1^2\right]=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(2y-1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x-2=0\\2y-1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=\frac{1}{2}\end{cases}}}\)
Vậy....
11 tháng 4 2020
Bài làm
a) 4x - 8y
<=> 4( x - 2y )
b) 12x( x - 2y ) - 8y( x - 2y )
<=> ( 12x - 8y )( x - 2y )
<=> 4( 3x - 2y )( x - 2y )
c) 2x + 2y - x2 - xy
= 2( x + y ) - x( x + y )
= ( x + y )( 2 - x )
d) x2 - 4y2
<=> ( x - 2y )( x + 2y )
e) x3 + x2y - 4x - 4y
<=> x2( x + y ) - 4( x + y )
<=> ( x - 2 )( x + 2 )( x + y )
g) 3x2 - 6xy + 3y2 - 12x3
<=>3( x2 - 3xy + y2 - 4x3 )
# Học tốt #
DT
11 tháng 4 2020
a)4(x-2y)
b)(x-2y)(12x-8y)
=4(x-2y)(3x-2y)
c)2(x+y)-x(x+y)
=(2-x)(x+y)
d)(x-2y)(x+2y)
e)x2(x+y)-4(x+y)
=(x+y)(x2-4)
=(x+y)(x-2)(x+2)
g)3(x2-2xy+y2-4z3)
=3[(x-y)2-4z3]
????????????phải là 4z2chứ nhỉ.....
ta có x^2 + 4x - 4y^2 + 8y = x^2 + 4x + 4 - ( 4y^2 - 8y^2 + 4) = (x+2)^2 - (2y-2)^2