Giúp mình câu c với ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)

a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)

c, \(2H_2+O_2 \rightarrow2H_2O\)
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5(mol) \Rightarrow n_{O_2}=0,75(mol)\)
\(V_{O_2}=22,4.0,75=16,8(l)\)
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5\left(mol\right)\)
a. PTHH: \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
Theo PTHH: \(n_{Fe}=n_{H_2}=1,5\left(mol\right)\)
\(\Rightarrow m_{Fe}=56\cdot1,5=84\left(g\right)\)
b. Đổi: \(500ml=0,5l\)
\(CM_{H_2SO_4}=\dfrac{1,5}{0,5}=3M\)
c. \(2H_2+O_2\rightarrow2H_2O\)
Theo PTHH: \(n_{O_2}=\dfrac{1}{2}n_{H_2}=\dfrac{1}{2}\cdot1,5=0,75\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,75\cdot22,4=16,8\left(l\right)\)


\(a,A=\dfrac{5x-15+2x+6-3x^2+2x+9}{\left(x-3\right)\left(x+3\right)}=\dfrac{-3x^2+9x}{\left(x-3\right)\left(x+3\right)}\\ A=\dfrac{-3x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{-3x}{x+3}\\ b,\left|x-2\right|=1\Leftrightarrow\left[{}\begin{matrix}x-2=1\\2-x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\\ \Leftrightarrow A=\dfrac{-3\cdot1}{1+3}=\dfrac{-3}{4}\\ c,A=\dfrac{-3\left(x+3\right)+9}{x+3}=-3+\dfrac{9}{x+3}\in Z\\ \Leftrightarrow x+3\inƯ\left(9\right)=\left\{-9;-3;-1;1;3;9\right\}\\ \Leftrightarrow x\in\left\{-12;-6;-4;-2;0;6\right\}\left(tm\right)\)

Lời giải:
a. Khi $x=64$ thì: $Q=\frac{\sqrt{64}-2}{\sqrt{64}-3}=\frac{8-2}{8-3}=\frac{6}{5}$
b.
\(P=\frac{x}{(\sqrt{x}-2)(\sqrt{x}+2)}+\frac{\sqrt{x}+2}{(\sqrt{x}-2)(\sqrt{x}+2)}+\frac{\sqrt{x}-2}{(\sqrt{x}+2)(\sqrt{x}-2)}\)
\(=\frac{x+\sqrt{x}+2+\sqrt{x}-2}{(\sqrt{x}+2)(\sqrt{x}-2)}=\frac{x+2\sqrt{x}}{(\sqrt{x}+2)(\sqrt{x}-2)}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}=\frac{\sqrt{x}}{\sqrt{x}-2}\)
Ta có đpcm.
c. \(K=Q(P-1)=\frac{\sqrt{x}-2}{\sqrt{x}-3}.(\frac{\sqrt{x}}{\sqrt{x}-2}-1)=\frac{\sqrt{x}-2}{\sqrt{x}-3}.\frac{2}{\sqrt{x}-2}=\frac{2}{\sqrt{x}-3}\)
$K=m+1$
$\Leftrightarrow \frac{2}{\sqrt{x}-3}=m+1$
$\Leftrightarrow m=\frac{2}{\sqrt{x}-3}-1$
Với $m=0$ (stn nhỏ nhất) thì $\frac{2}{\sqrt{x}-3}-1=m$ có nghiệm $x=25$
Vậy stn $m$ cần tìm là $0$

Nếu là câu c
c, Ta có : BD là phân giác \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(1\right)\)
Ta có : BK là phân giác \(\widehat{ABH}\)
\(\Rightarrow\dfrac{HK}{AK}=\dfrac{BH}{AB}\left(2\right)\)
Ta có: ΔHBA ~ ΔABC (cmt )
(*nếu chưa c/m tam giác đồng dạng thì hãy c/m, làm r thì khỏi )
\(\Rightarrow\dfrac{HB}{AB}=\dfrac{AB}{AC}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\dfrac{AD}{DC}=\dfrac{HK}{AK}\)
\(\Rightarrow AK.AD=HK.CD\left(đpcm\right)\)

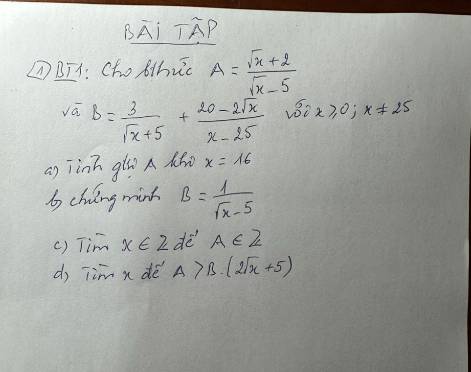
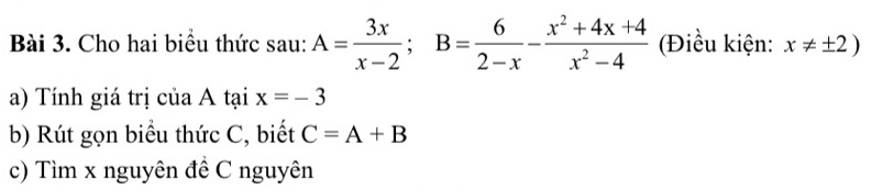

 giúp mình câu c với ạ, 2 câu trên mình biết làm rồi
giúp mình câu c với ạ, 2 câu trên mình biết làm rồi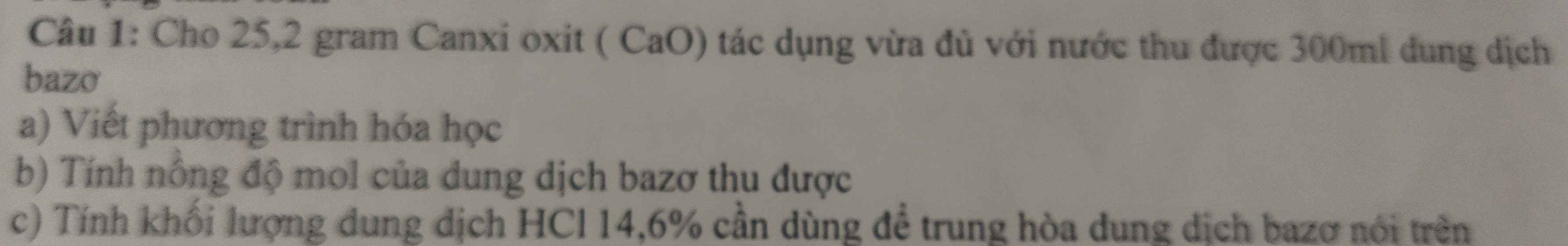
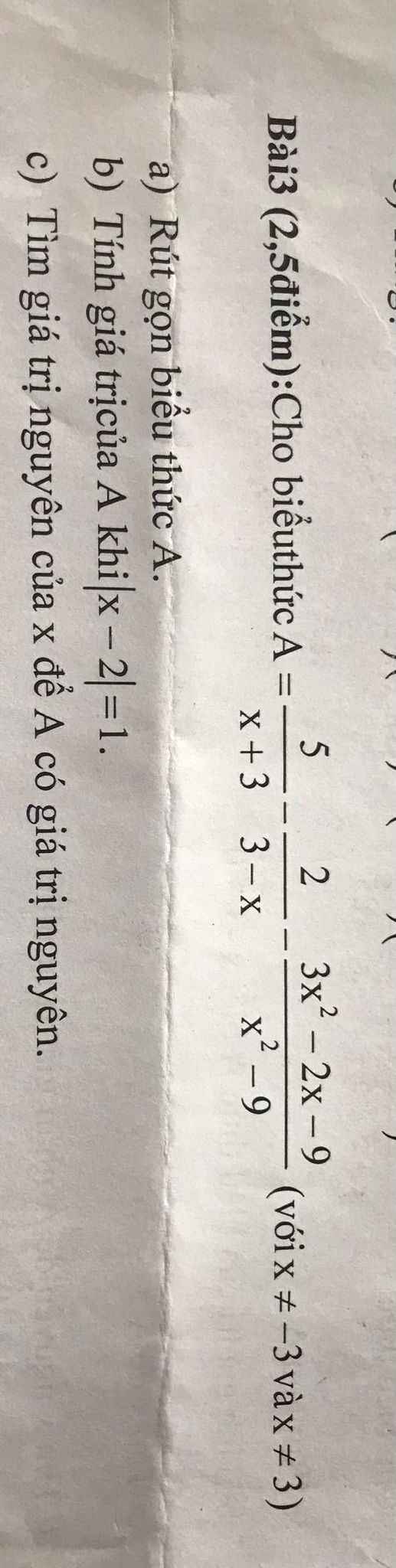
 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 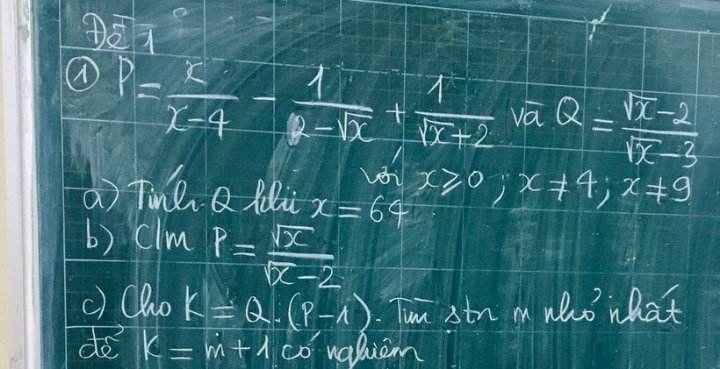 giúp mình câu c với ạ, mình cảm ơn nhiều
giúp mình câu c với ạ, mình cảm ơn nhiều giải giúp mình câu c với ạ, mình cảm ơnnnnn
giải giúp mình câu c với ạ, mình cảm ơnnnnn
a: XétΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔAMI vuông tại I và ΔADI vuông tại I có
AI chung
MI=DI
Do đó: ΔAMI=ΔADI
Suy ra: AM=AD
vì AM⊥BC tại M
=>ΔABM vuông tại M và ΔACM vuông tại M
XétΔABM vuông tại M và ΔACM vuông tại M ta có
AB=AC
\(\widehat{AMB}=\widehat{AMC=90^o}\)
cạnh AM chung
=> ΔABM=ΔACM(c.h-c.g.v)
ta có MI⊥AC
==>t ΔAMI vuông tại I và ΔADI vuông tại I
Xét ΔAMI vuông tại I và ΔADI vuông tại I ta có
AI chung
\(\widehat{AIM}=\widehat{AID}=90^o\)
MI=DI
==>ΔAMI=ΔADI
==> AM=AD(2 cạnh tg ứng)