Cho hình lăng trụ đều ABCD.A'B'C'D' có cạnh bằng a. Các điểm E, F thay đổi lần lượt thuộc các cạnh BB', DD' sao cho \(\left(EAC\right)\perp\left(FAC\right)\). Tìm giá trị nhỏ nhất của \(V_{ACEF}?\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)

Gọi H là hình chiếu vuông góc của A' lên (ABCD)
Do \(A'A=A'B=A'D\) \(\Rightarrow H\) trùng tâm đường tròn ngoại tiếp tam giác ABD
\(\Rightarrow H\) là trung điểm BD
\(AC=\sqrt{AB^2+AD^2}=2a\)\(\Rightarrow AH=\dfrac{1}{2}AC=a\)
\(\Rightarrow A'H=\sqrt{A'A^2-AH^2}=a\sqrt{3}\)
\(\Rightarrow V=A'H.AB.AD=3a^3\)

\(AA'=\dfrac{2a}{\sqrt{3}}\)
\(V=AA'\cdot S_{ABCD}=\dfrac{16a^3}{\sqrt{3}}\)

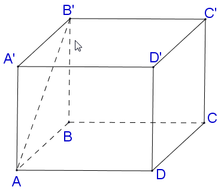
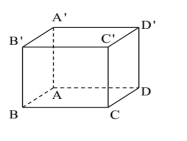
\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)
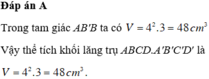

 A.3a3 B.a3 C.a3
A.3a3 B.a3 C.a3
Gọi O là giao điểm AC và BD
Do lăng trụ đều \(\Rightarrow AC\perp\left(BDD'B'\right)\Rightarrow AC\perp\left(EOF\right)\)
\(V_{ACEF}=V_{AOEF}+V_{COEF}=2V_{AOEF}=\dfrac{2}{3}AO.S_{OEF}=\dfrac{a\sqrt{2}}{3}.S_{OEF}\)
Đặt \(BE=x;\) \(DF=y\), trên BB' lấy G sao cho \(BG=DF=y\)
\(\Rightarrow FG=BD=a\sqrt{2}\) và \(EG=\left|x-y\right|\)
\(\Rightarrow EF=\sqrt{EG^2+FG^2}=\sqrt{2a^2+\left(x-y\right)^2}\)
\(OE=\sqrt{OB^2+BE^2}=\sqrt{\dfrac{a^2}{2}+x^2}\) ; \(OF=\sqrt{OD^2+DF^2}=\sqrt{\dfrac{a^2}{2}+y^2}\)
Do \(\left(EAC\right)\perp\left(FAC\right)\Rightarrow OE\perp OF\)
\(\Rightarrow OE^2+OF^2=EF^2\)
\(\Rightarrow a^2+x^2+y^2=2a^2+\left(x-y\right)^2\Rightarrow xy=\dfrac{a^2}{2}\)
\(S_{OEF}=\dfrac{1}{2}OE.OF=\dfrac{1}{2}\sqrt{\left(\dfrac{a^2}{2}+x^2\right)\left(\dfrac{a^2}{2}+y^2\right)}=\dfrac{1}{2}\sqrt{\dfrac{a^4}{4}+\left(xy\right)^2+\dfrac{a^2}{2}\left(x^2+y^2\right)}\)
\(=\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+\dfrac{a^2}{2}\left(x^2+y^2\right)}\ge\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+\dfrac{a^2}{2}.2xy}=\dfrac{1}{2}\sqrt{\dfrac{a^4}{2}+a^2.\dfrac{a^2}{2}}=\dfrac{a^2}{2}\)
\(\Rightarrow V_{ACEF}\ge\dfrac{a\sqrt{2}}{3}.\dfrac{a^2}{2}=\dfrac{a^3\sqrt{2}}{6}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{a\sqrt{2}}{2}\)