-x3 + 3x2 -3x +1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2021
1a) \(=-\left(x^3-3x^2+3x-1\right)=-\left(x-1\right)^3\)
b) \(=-\left(x^3-3x^2+3x-1\right)=-\left(x-1\right)^3\)
7 tháng 11 2021
\(a,=-\left(x-1\right)^3\left[=\left(1-x\right)^3\right]\\ b,=\left(1-x\right)^3\)
NN
3
CC
19 tháng 10 2021
Bạn phải vt thêm dấu mũ vào mới giải đc chứ!! Để thế kia ai mà giải đc
H
2
14 tháng 8 2021
a: Ta có: \(\left(x^2+2\right)\left(x-4\right)-\left(x+2\right)^3=-16\)
\(\Leftrightarrow x^3-4x^2+2x-8-x^3-6x^2-12x-8=-16\)
\(\Leftrightarrow-10x^2-10x=0\)
\(\Leftrightarrow-10x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
c: Ta có: \(x^3+3x^2+3x+28=0\)
\(\Leftrightarrow\left(x+1\right)^3=-27\)
\(\Leftrightarrow x+1=-3\)
hay x=-4
25 tháng 6 2019
\(\left(x^3-3x^2+3x-1\right)\)
\(=x^3-3x^2.1+3x.\left(-1\right)^2-1^3\)
\(=\left(x-1\right)^3\)
25 tháng 6 2019
(x+a)3=x3+(a+a+a)x2+(a.a+a.a+a.a)x+a3
(x−1)3→a=−1
⇒(x−1)3=x3+(−1−1−1)x2+(1+1+1)x+(−1)3
=x3−3x2+3x−1
27 tháng 9 2021
\(x^3+3x^2=-3x-1\)
\(\Leftrightarrow x^3+3x^2+3x+1=0\)
\(\Leftrightarrow\left(x+1\right)^3=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
28 tháng 1 2022
a, \(A=2x^3-9x^5+3x^5-3x^2+7x^2-12=-6x^5+2x^3+4x^2-12\)
b, \(B=2x^4+x^2+2x-2x^3-2x^2+x^2-2x+1=2x^4-2x^3+1\)
c, \(C=2x^2+x-x^3-2x^2+x^3-x+3=3\)
N
3
24 tháng 10 2021
a) \(\Rightarrow\left(x-1\right)^3=0\Rightarrow x=1\)
b) \(\Rightarrow\left(x^3-1\right)\left(x^3+1\right)=0\Rightarrow\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)(do \(\left\{{}\begin{matrix}x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\\x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\end{matrix}\right.\))
c) \(\Rightarrow4x\left(x^2-9\right)=0\Rightarrow4x\left(x-3\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
d) \(\Rightarrow\left(x-2\right)^3=0\Rightarrow x=2\)
24 tháng 10 2021
a) \(x^3-3x^2+3x-1=0\Rightarrow\left(x-1\right)^3=0\Rightarrow x-1=0\)
\(\Rightarrow x=1\)
b) \(x^6-1=0\Rightarrow\left(x^3\right)^2-1=0\Rightarrow\left(x^3-1\right)\left(x^3+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x^3-1=0\\x^3+1=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
c) \(4x^3-36x=0\Rightarrow4x\left(x^2-36\right)=0\Rightarrow4x\left(x-6\right)\left(x+6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}4x=0\\x-6=0\\x+6=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=6\\x=-6\end{matrix}\right.\)
d) \(x^3-6x^2+12x-8=0\) (đề bài như vậy mới làm đc, nếu là +8 thì mình xin bó tay nhé)
\(\Rightarrow x^3-3\cdot x^2\cdot2+3\cdot x\cdot2^2-2^3=0\)
\(\Rightarrow\left(x-2\right)^3=0\Rightarrow x-2=0\Rightarrow x=2\)
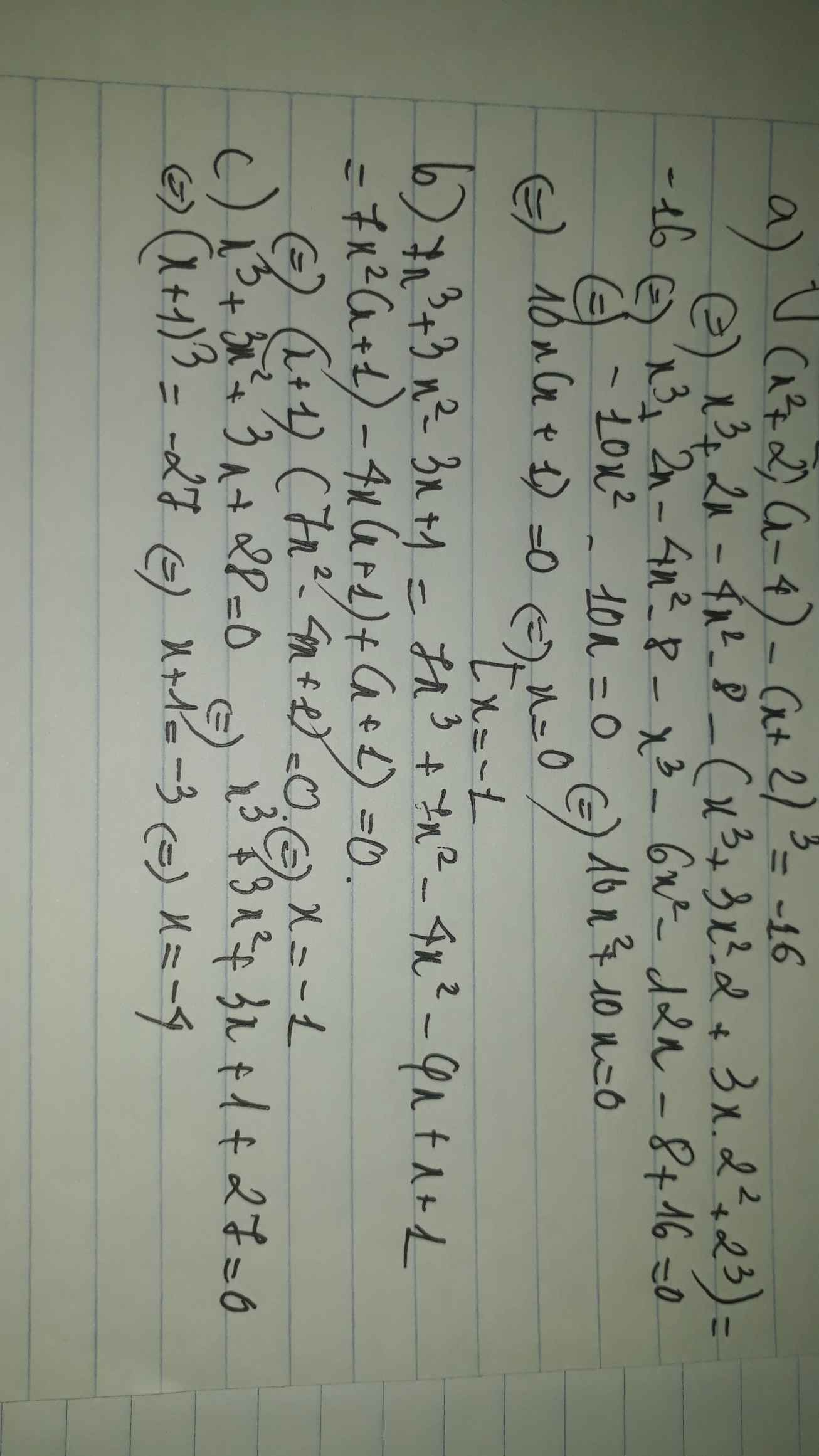
-x3+3x2-3x+1
=> - (x3 - 3x2 + 3x - 1)
=> - (x - 1)3
cho xin dấu (k)
Ta có - (x3 - 3x2 + 3x - 1) = - (x - 1)3