dựng hình bình hành ABCD biết điểm A ;trung điểm BC,CD lần lượt là E,F
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
14 tháng 7 2018
Cách dựng
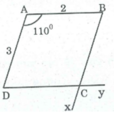
- Dựng ΔABD có AB = 2cm, ∠A = 110o, AD = 3cm
- Dựng tia Bx //AD
- Dựng tia Dy // AB và Dy cắt Bx tại C
Ta có hình bình hành ABCD cần dựng
Chứng minh
AB //CD, AD // BC nên tứ giác ABCD là hình bình hành.
Ta lại có: AB = 2cm, ∠ A = 110 0 , AD = 3cm.
Bài toán có một nghiệm hình.
PT
1
CM
11 tháng 1 2018
Cách dựng
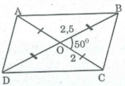
- Dựng ∆ OBC có OC = 2cm, OB = 2,5 cm, ∠ (BOC) = 50 0
- Trên tia đối tia OC lấy điểm A sao cho OA = OC = 2cm
- Trên tia đối tia OB lấy điểm D sao cho OD = OB =2,5cm
Nối AB, BC, CD, AD ta có hình bình hành ABCD cần dựng
Chứng minh
Tứ giác ABCD có OA = OC, OB = OD nên nó là hình bình hành vì có 2 đường chéo cắt nhau tại trung điểm mỗi đường.
Có AC = 4cm , BD = 5cm, ∠ (BOC) = 50 0
Bài toán có một nghiệm hình
CM
26 tháng 5 2017
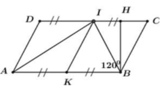
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.
=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm
Xét tứ giác KICB ta có:
IC = BC = KB = IK = 1 2 AB = 10cm
=> IKBC là hình thoi (dấu hiệu nhận biết).
Mà B ^ = 1200 => I C B ^ = 1800 – 1200 = 600
Xét tam giác ICB có: I C = B C I C B = 60 0
=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = 1 2 BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm
=> SABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm2
Đáp án cần chọn là: A
17 tháng 8 2017
Em tự vẽ hình nhé. Như sau:
Dễ thấy \(\widehat{AEB}=\widehat{CEF}=60^o\)nên \(\widehat{BEC}=\widehat{AEF}\)
Lại có \(\Delta AEB\)đều nên EA=EB. \(\Delta CEF\)đều nên EC=EF
Do đó \(\Delta EBC=\Delta EAF\left(c-g-c\right)\)=> BC=AF
\(\Delta ADF\)đều nên AF=AD
=> BC=AD (=AF)
Cmtt:CD=AB
Vậy ABCD là hbh
CM
26 tháng 11 2017
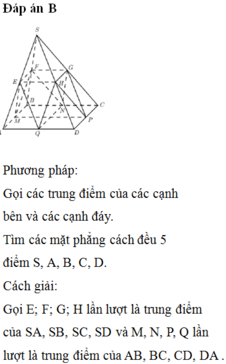
Đáp án D
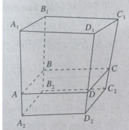
Tồn tại 5 mặt phẳng thỏa mãn đề bài là:
- Mp đi qua trung điểm AD,BC,SC,SD
- Mp đi qua trung điểm CD,AB,SC,SB
- Mp đi qua trung điểm AD,BC,SB,SA
- Mp đi qua trung điểm CD,AB,SA,SD
- Mp đi qua trung điểm SA,SB,SC,SD
mình không nhớ rõ các bước của 1 bài toán dựng hình
nên mình chỉ làm phần dựng hình và cơ sở thôi nhé
a/
gọi M,N,P là trung điểm CD,AB,AD
lấy I là trung điểm MN, lấy đối xứng P qua I ta đc Q
là trung điểm BC
qua P,Q kẻ các dg thẳng //MN
qua M,N kẻ các dg thẳng //PQ
giao điểm các dg thẳng là A,B,C,D là đỉnh hbh
cơ sở:
hbh ABCD có trung điểm các cạnh M,N,P,Q
=>MN//BC//AD , PQ//CD//AB
và I là trọng tâm hbh
=>IQ=IP, IM=IN
b/
lấy I là trung điểm EF , nối AI
trên tia AI lấy O sao AO=2/3AI
lấy C sao AC=4/3 AI
nối CF,CE
qua A kẻ AD//CE cắt CF tại D
kẻ AB//CF cắt CE tại B
cơ sở:
hbh ABCD có O là trọng tâm,E,F là trung điểm BC,DC
I là trung điểm EF
=>EO//CF, CE//FO =>OECF là hbh
=>trubg điểm I của EF là trung điểm OC
hbh ABCD có AC là dg chéo
=>AO=OC=2OI=2IC
=>AC=4/3AI, AO=2/3AI
tử đó bạn làm theo các bước của bài toán dựng hình nha