Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

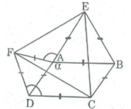
Ta có:
∠ (BAD) + ∠ ∠ (ADC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ADC) = 180 0 - ∠ (BAD) = 180 0 – α
∠ (CDF) = ∠ (ADC) + ∠ (ADF) = 180 0 - α 2 + 60 0 = 240 0 - α
Suy ra: ∠ (CDF) = ∠ (EAF)
Xét ∆ AEF và ∆ DCF: AF = DF ( vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
∠ (CDF) = ∠ (EAF) (chứng minh trên)
Do đó: ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
∠ (CBE) = ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
∠ (CBE) = ∠ (CDF) = 240 0 - α
BC = DF (vì cùng bằng AD)
Do đó ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ∆ ECF đều.

K D E B C
Không làm mất tính tổng quát, xét tam giác ABC có góc \(\widehat{A}>90^o\)như trên hình vẽ.
Xét tam giác CAB và CEK có \(CA=CE;CB=CK;\widehat{ACB}=\widehat{CEK}=60^o-\widehat{ACK}\)
Do đó, \(\Delta ACB=\Delta ECK.c.g.c\Rightarrow EK=AB=AD\)
Tương tự cũng có:
\(DK=AC=AE\)
Vậy: ADKE có \(EK=AD;DK=AE\)nên là hình bình hành.
Em tự vẽ hình nhé. Như sau:
Dễ thấy \(\widehat{AEB}=\widehat{CEF}=60^o\)nên \(\widehat{BEC}=\widehat{AEF}\)
Lại có \(\Delta AEB\)đều nên EA=EB. \(\Delta CEF\)đều nên EC=EF
Do đó \(\Delta EBC=\Delta EAF\left(c-g-c\right)\)=> BC=AF
\(\Delta ADF\)đều nên AF=AD
=> BC=AD (=AF)
Cmtt:CD=AB
Vậy ABCD là hbh