Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(\widehat{AFH}=90^0\) (góc nt chắn nửa đg tròn) nên \(HF\perp AB\)
Lại có H là trực tâm tam giác ABC nên HF và HC là đường cao tam giác ABC \(\left(HF\perp AB\right)\)
Suy ra C,H,F thẳng hàng hay CF là đường cao tam giác ABC
\(\Delta AFC=\Delta AEB\left(ch-gn\right)\\ \Rightarrow AE=AF\\ \Rightarrow\widehat{AFE}=\widehat{ABC}\left(2\Delta.cân.chung.đỉnh.A\right)\)
Mà 2 góc này ở vị trí đồng vị nên EF//BC

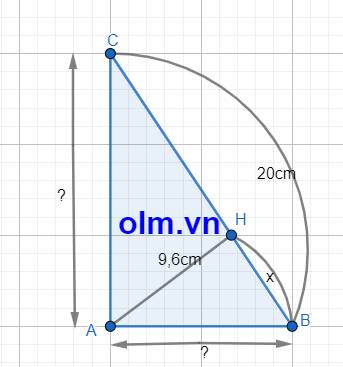
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên \(x\) < CH
Xét tam giác vuông HAB vuông tại H theo pytago ta có:
AB2 = HA2 + HB2 = 9,62 + \(x^2\) = 92,16 + \(x^2\)
Xét tam giác vuông AHC vuông tại H theo pytago ta có:
AC2 = HA2 + HC2 = 9,62 + (\(20-x\))2 = 92,16 + 400 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(x\) + \(x^2\)
Xét tam giác vuông ABC vuông tại A theo pytago ta có:
AC2 + AB2 = BC2
492,16 - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 202
(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0
2\(x^2\) - 40\(x\) + 584,32 - 400 = 0
2\(x^2\)- 40\(x\) + 184,32 =0
\(x^2\) - 20\(x\) + 92,16 = 0
△' = 102 - 92,16 = 7,84 > 0
\(x\)1 = -(-10) + \(\sqrt{7,84}\) = 12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH (loại )
\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)
Thay \(x_2\) = 7,2 vào biểu thức: AB2 = 92,16 + \(x^2\) = 92,16 + 7,22 = 144
⇒AB = \(\sqrt{144}\) = 12
Thay \(x_2\) = 7,2 vào biểu thức: AC2 = 492,16 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(\times\) 7,2 + 7,22 = 256
AC = \(\sqrt{256}\) = 16
Kết luận AB = 12 cm; AC = 16 cm

Vì △ABC có AB = BC (gt) => △ABC cân tại B => BAC = BCA => BAC : 2 = BCA : 2 => BAM = BCN
Xét △BAM và △BCN
Có: ABC là góc chung
AB = BC (gt)
BAM = BCN (cmt)
=> △BAM = △BCN (g.c.g)
=> BM = BN (2 cạnh tương ứng)
=> △BMN cân tại B
=> BNM = (180o - NBM) : 2
Vì △ABC cân tại B => BAC = (180o - ABC) : 2
=> BNM = BAC
Mà 2 góc này nằm ở vị trí so le trong
=> MN // AC (dhnb)