Nếu \(a+b+c=0\) thì \(a^3+b^3+c^3=...\)
Giải bằng phương pháp tự luận
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 8 2019
Ta có M=a(b+c)+3b(c+a)+5c(a+b)=a(3-a)+3b(3-b)+5c(3-c)=\(\frac{81}{4}\)-\(\left(a-\frac{3}{2}\right)^2+3\left(b-\frac{3}{2}\right)^2+5\left(c-\frac{3}{2}\right)^2\)
Đặt x=\(\left|a-\frac{3}{2}\right|\),y=\(\left|b-\frac{3}{2}\right|\),z=\(\left|c-\frac{3}{2}\right|\)=>x+y+z\(\ge\left|a+b+c-\frac{9}{2}\right|=\frac{3}{2}\)
Khi đó M=\(\frac{81}{4}-\left(x^2+3y^2+5z^2\right)\)
Đưa thêm các tham số\(\alpha,\beta,\gamma>0\)Áp dụng bất đẳng thức AM-GM:\(x^2+\alpha^2\ge2x\alpha\)(1);\(3y^2+3\beta^2\ge6y\beta\)(2);\(5z^2+5\gamma^2\ge10z\gamma\)(3)
Suy ra: \(M-\alpha^2-3\beta^2-5\gamma^2\le\frac{81}{4}-2\left(x\alpha+3y\beta+5z\gamma\right)\)
Ta chọn \(\alpha=3\beta=5\gamma\)\(\Rightarrow M\le\frac{81}{4}+\alpha^2+3\beta^2+5\gamma^2-2\alpha\left(x+y+z\right)\)\(\le\frac{81}{4}+\alpha^2+3\beta^2+5\gamma^2-3a\)
Ta thấy dấu bằng các bất đẳng thức (1),(2),(3) xảy ra khi \(x=\alpha,y=\beta,z=\gamma\)\(\Rightarrow\alpha+\beta+\gamma=\alpha+\frac{\alpha}{3}+\frac{\alpha}{5}=x+y+z=\frac{3}{2}\)\(\Rightarrow\alpha=\frac{45}{46}\),\(\beta=\frac{15}{46},\gamma=\frac{9}{46}\)
Vậy MaxM=\(\le\frac{81}{4}+\left(\frac{45}{46}\right)^2+3\left(\frac{15}{46}\right)^2+5\left(\frac{9}{46}\right)^2-3.\frac{45}{46}\)=\(\frac{432}{23}\)
CN
0
CM
13 tháng 7 2018
Chọn D.
Giả sử z1; z2 là nghiệm của phương trình đã cho với |z| = 1.
Theo định lý Viet ta có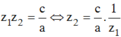 
.Suy ra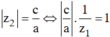 
Bởi vì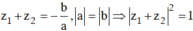 
, suy ra 
16 tháng 9 2018
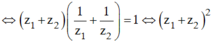
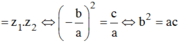
\(a)\)\(\left(a+b+c+d\right)\left(a-b-c+d\right)=\left(a-b+c-d\right)\left(a+b-c-d\right)\)
\(\Leftrightarrow\)\(\frac{a+b+c+d}{a-b+c-d}=\frac{a+b-c-d}{a-b-c+d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a+b+c+d}{a-b+c-d}=\frac{a+b-c-d}{a-b-c+d}=\frac{a+b+c+d+a+b-c-d}{a-b+c-d+a-b-c+d}=\frac{2\left(a+b\right)}{2\left(a-b\right)}=\frac{a+b}{a-b}\) \(\left(1\right)\)
Lại có :
\(\frac{a+b+c+d}{a-b+c-d}=\frac{a+b-c-d}{a-b-c+d}=\frac{a+b+c+d-a-b+c+d}{a-b+c-d-a+b+c-d}=\frac{2\left(c+d\right)}{2\left(c-d\right)}=\frac{c+d}{c-d}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)\(\Leftrightarrow\)\(\frac{a+b}{c+d}=\frac{a-b}{c-d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a+b}{c+d}=\frac{a-b}{c-d}=\frac{a+b+a-b}{c+d+c-d}=\frac{2a}{2c}=\frac{a}{c}\) \(\left(3\right)\)
Lại có :
\(\frac{a+b}{c+d}=\frac{a-b}{c-d}=\frac{a+b-a+b}{c+d-c+d}=\frac{2b}{2d}=\frac{b}{d}\) \(\left(4\right)\)
Từ \(\left(3\right)\) và \(\left(4\right)\) suy ra \(\frac{a}{c}=\frac{b}{d}\) ( đpcm )
Chúc bạn học tốt ~
16 tháng 9 2018
\(b)\)\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow\)\(a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
\(\Leftrightarrow\)\(a^2+b^2+c^2-ab-bc-ca=0\) ( vì \(a+b+c=0\) )
\(\Leftrightarrow\)\(2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\)\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\)\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\)\(\hept{\begin{cases}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\\\left(c-a\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}\Leftrightarrow}\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}\Leftrightarrow}a=b=c}\)
Vậy ...
Chúc bạn học tốt ~
29 tháng 9 2019
a ) \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
Nếu : \(a+b+c=0\) thì đẳng thức trên đúng .
\(\Rightarrowđpcm\)
b ) \(a+b+c+d=0\)
\(\Rightarrow a+b=-\left(c+d\right)\Leftrightarrow\left(a+b\right)^3=-\left(c+d\right)^3\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=-3ab\left(a+b\right)-3cd\left(c+d\right)\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=3ab\left(c+d\right)-3cd\left(c+d\right)\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=3\left(c+d\right)\left(cb-cd\right)\left(đpcm\right)\)
Chúc bạn học tốt !!!
29 tháng 9 2019
a ) a^3+b^3+c^3=3abca3+b3+c3=3abc
\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0⇔(a+b)3+c3−3ab(a+b)−3abc=0
\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0⇔(a+b+c)(a2+b2+c2−ab−bc−ac)=0
Nếu : a+b+c=0a+b+c=0 thì đẳng thức trên đúng .(đpcm)
b ) a+b+c+d=0a+b+c+d=0
\Rightarrow a+b=-\left(c+d\right)\Leftrightarrow\left(a+b\right)^3=-\left(c+d\right)^3⇒a+b=−(c+d)⇔(a+b)3=−(c+d)3
\Leftrightarrow a^3+b^3+c^3+d^3=-3ab\left(a+b\right)-3cd\left(c+d\right)⇔a3+b3+c3+d3=−3ab(a+b)−3cd(c+d)
\Leftrightarrow a^3+b^3+c^3+d^3=3ab\left(c+d\right)-3cd\left(c+d\right)⇔a3+b3+c3+d3=3ab(c+d)−3cd(c+d)
\Leftrightarrow a^3+b^3+c^3+d^3=3\left(c+d\right)\left(cb-cd\right)\left(đpcm\right)⇔a3+b3+c3+d3=3(c+d)(cb−cd)(đpcm)
5 tháng 11 2017
ta có:a^3+b^3+c^3=3abc
<=>(a+b)^3+c^3-3ab(a+b)-3abc=0
<=>(a+b+c)[(a+b)^2+(a+b)c+c^2]-3ab(a+b...
<=>(a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0
<=>1/2(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]...
do a,b,c doi mot khac nhau nen PT<=>a+b+c=0(DPCM)
31 tháng 8 2019
Gọi x, y, z (h) lần lượt là A, B, C làm một mình để xong công việc.
Nếu A và B cùng làm thì hết 6 giờ => 6/x + 6/y =1
nếu B và C cùng làm thì hết 4,5 giờ => 4,5/y +4,5/z =1
nếu A và C làm thì chỉ hết 3h36' = 3,6h => 3,6/x + 3,6/z = 1
=> 1/x = 1/9 ; 1/y=1/18; 1/z=1/6
=> x=9 ; y=18; z=6
Nếu A, B, C cùng làm thì mất a (h) để hoàn thành công việc.
=> a(1/x + 1/y + 1/z) = 1 => 1/x + 1/y + 1/z = 1/a
=> 1/a = 1/9 +1/18 + 1/6 = 1/3 => a=3
Vậy Nếu A, B, C cùng làm thì mất 3h để hoàn thành công việc
Taco:a3+b3=(a+b)3-3ab(a+b)=>a3+b3+c3=(-c)3+3abc+c3=3abc(thaya+b=-c)