Vẽ giúp mình hình bài này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ

CA=CB
DA=DB
Do đó: CD là trung trực của BA(1)
EA=EB
=>E nằm trên trung trực của AB(2)
Từ (1), (2) suy ra C,D,E thẳng hàng

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành

\(3x=4z\Rightarrow\dfrac{x}{4}=\dfrac{z}{3}\); \(\dfrac{x}{5}=\dfrac{y}{6}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}=\dfrac{x-y+z}{20-24+15}=\dfrac{121}{11}=11\)
\(\Rightarrow x=20.11=220;z=15.11=165;y=264\)

có : \(AH\perp BD\)
\(CK\perp DB\) =>AH//CK
Có : tứ giác ABCD là hình bình hành :
`=>` AB//CB
`=> góc ADB = góc gocd DBC
Xét tam giác `ADH` và tam giác `CBK` có
`AB = CB`(tứ giác ABCD là hbh)
`AHD = CKB = 90^0`
`ADH = CBK(c/mt)`
`=> tam giác ADH = tam giác BCK(ch-gn)
`=> AH = CK`(t/ứng)
xét tg BHCK có :
`AH = Ck`
`AH//CK`
`=> tg BHCK là hình bình hành

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2
 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn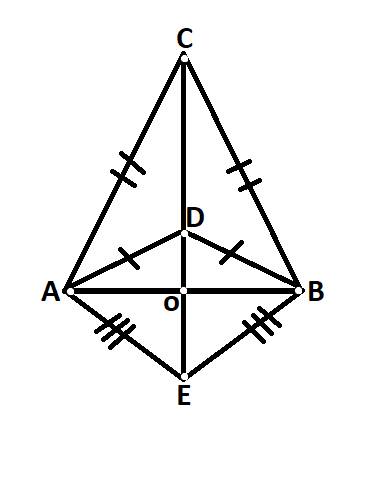





 làm cho mình 2 bài này với ạ vẽ hình cho mình nhé
làm cho mình 2 bài này với ạ vẽ hình cho mình nhé 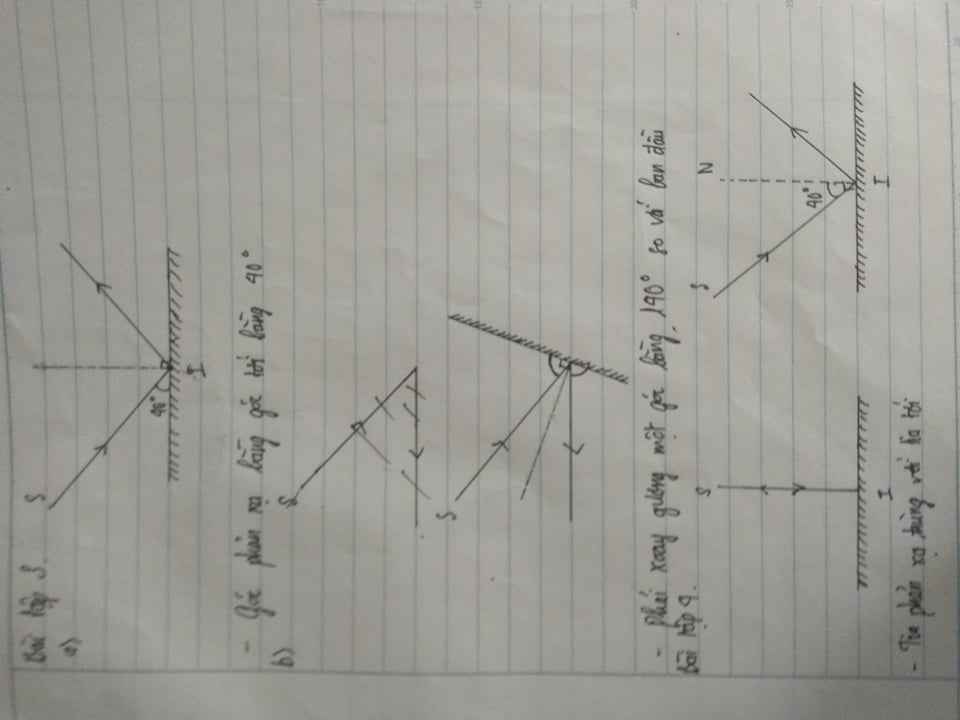
 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ