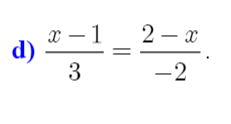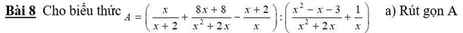Trình bày chi tiết ra hộ mik vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bạn An góp số phần tổng số tiền bốn bạn là:
\(1\div\left(1+2\right)=\frac{1}{3}\)(tổng số tiền)
Bạn Bình góp số phần tổng số tiền bốn bạn là:
\(1\div\left(1+3\right)=\frac{1}{4}\)(tổng số tiền)
Bạn Cường góp số phần tổng số tiền bốn bạn là:
\(1\div\left(1+4\right)=\frac{1}{5}\)(tổng số tiền)
Bạn Dũng góp số phần tổng số tiền bốn bạn là:
\(1-\frac{1}{3}-\frac{1}{4}-\frac{1}{5}=\frac{13}{60}\)(tổng số tiền)
Giá tiền chiếc máy tính bỏ túi là:
\(15600\div\frac{13}{60}=72000\)(đồng)
Bạn An góp số tiền là:
\(72000\times\frac{1}{3}=24000\)(đồng)
Bạn Bình góp số tiền là:
\(72000\times\frac{1}{4}=18000\)(đồng)
Bạn Cường góp số tiền là:
\(72000\times\frac{1}{5}=14400\)(đồng)

Bạn tự vẽ hình nhé!
a, Xét \(\Delta ABC.và.\Delta ABH.có:\)
\(\widehat{BAC}=\widehat{BHA}\)
\(\widehat{B}.chung\)
\(\Rightarrow\Delta ABC\sim\Delta ABH\)
b, Áp dụng định lý Pytago vào tam giác vuông ABC, ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=4^2+5^2=41\\ \Rightarrow BC=\sqrt{41}\approx6,4\left(cm\right)\)
Vì \(\Delta ABC\sim\Delta ABH\) và \(\Delta ABC\) có đường cao AH:
\(\Rightarrow\dfrac{BH}{BA}=\dfrac{HC}{AC}\) ( 1 )
Dựa vào tính chất dãy tỉ số bằng nhau, ta lại có:
\(\left(1\right)\Rightarrow\dfrac{BH}{BA}=\dfrac{HC}{AC}=\dfrac{BH+HC}{BA+AC}=\dfrac{BC}{4+5}=\dfrac{6,4}{9}\)
\(\Rightarrow BH=\dfrac{4.6,4}{9}=2,8\left(cm\right)\)

\(\dfrac{x-1}{3}=\dfrac{2-x}{-2}\)
⇔ \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)
⇔ \(3x-6-2x+2=0\)
⇔ \(x-4=0\)
⇒ \(x=4\)

\(A=\left(\dfrac{x}{x+2}+\dfrac{8x+8}{x^2+2x}-\dfrac{x+2}{x}\right):\left(\dfrac{x^2-x-3}{x^2+2x}+\dfrac{1}{x}\right)\)
\(\Leftrightarrow A=\left(\dfrac{x^2}{x\left(x+2\right)}+\dfrac{8x+8}{x\left(x+2\right)}-\dfrac{\left(x+2\right)^2}{x\left(x+2\right)}\right):\left(\dfrac{x^2-x-3}{x\left(x+2\right)}+\dfrac{x+2}{x\left(x+2\right)}\right)\)
\(\Leftrightarrow A=\dfrac{x^2+8x+8-\left(x+2\right)^2}{x\left(x+2\right)}:\dfrac{x^2-x-3+x+2}{x\left(x+2\right)}\)
\(\Leftrightarrow A=\dfrac{x^2+8x+8-x^2-4x-4}{x\left(x+2\right)}:\dfrac{x^2-1}{x\left(x+2\right)}\)
\(\Leftrightarrow A=\dfrac{4x+4}{x\left(x+2\right)}.\dfrac{x\left(x+2\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow A=\dfrac{4\left(x+1\right)}{x\left(x+2\right)}.\dfrac{x\left(x+2\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow A=\dfrac{4}{x-1}\)
\(A=\dfrac{x^2+8x+8-x^2-4x-4}{x\left(x+2\right)}:\dfrac{x^2-x-3+x^2+2x}{x\left(x+2\right)}\)
\(=\dfrac{4\left(x+1\right)}{x-3}\)

\(A=\dfrac{31\cdot\left(31^{12}-1\right)}{31\left(31^{13}+1\right)}=\dfrac{31^{13}+1-32}{31\left(31^{13}+1\right)}=\dfrac{1}{31}-\dfrac{32}{31^{14}+31}\)
\(B=\dfrac{31\left(31^{13}-1\right)}{31\left(31^{14}+1\right)}=\dfrac{1}{31}-\dfrac{32}{31^{15}+31}\)
Dễ thấy \(31^{14}+31< 31^{15}+31\Rightarrow\dfrac{32}{31^{14}+31}>\dfrac{32}{31^{15}+31}\\ \Rightarrow\dfrac{1}{31}-\dfrac{32}{31^{14}+31}< \dfrac{1}{31}-\dfrac{32}{31^{15}+31}\)
Vậy A < B


Khối lượng lúa thu được là:
\(150\cdot50:100\cdot80=6000\left(kg\right)=60\left(tạ\right)\)

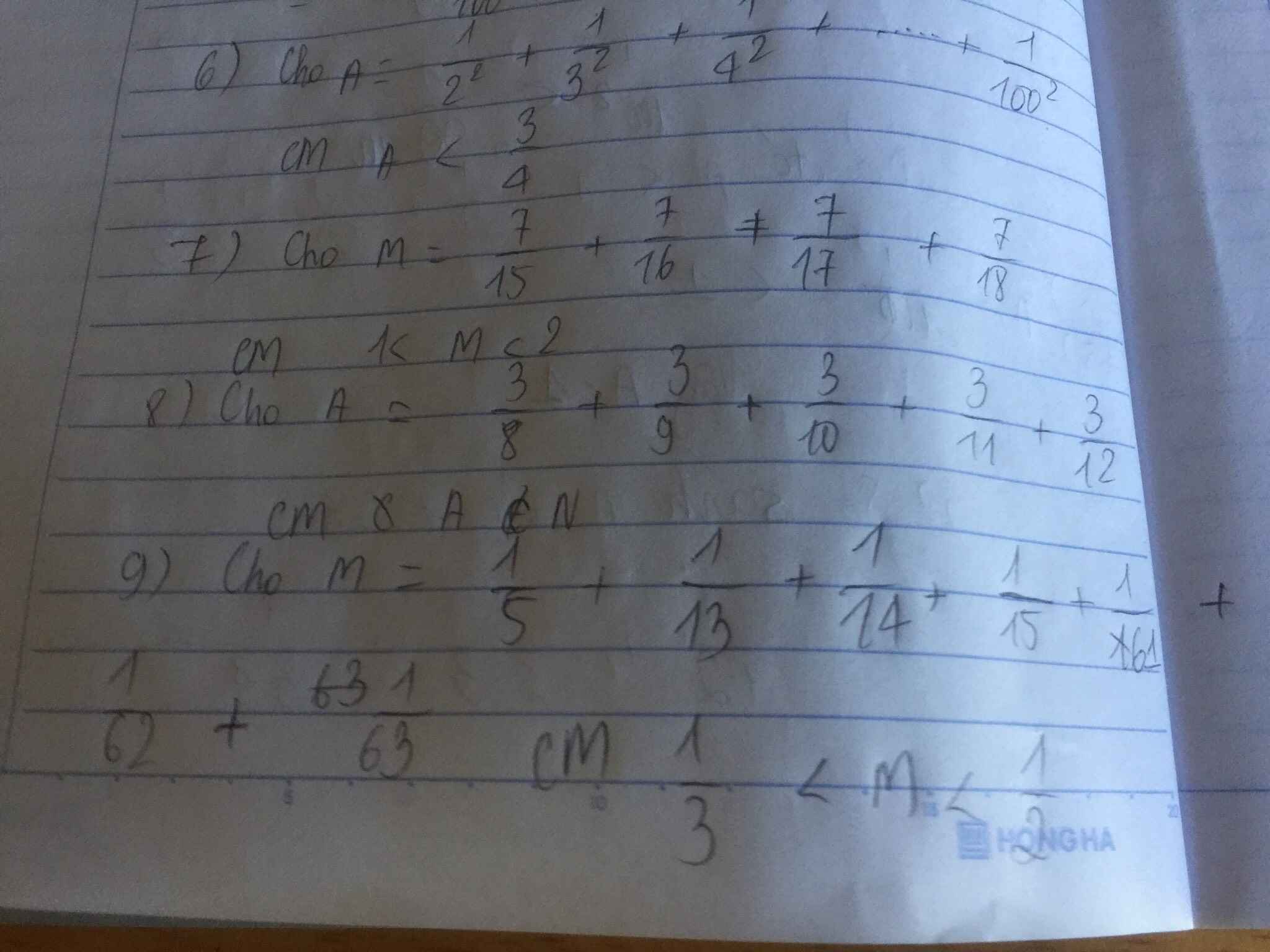
 Các bn giải chi tiết hộ mik vs
Các bn giải chi tiết hộ mik vs