Xin lời giải bài này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)

Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên

A = 4 + 4² + 4³ + ... + 4¹⁰⁰
⇒ 4A = 4² + 4³ + 4⁴ + ... + 4¹⁰¹
⇒ 3A = 4A - A
= (4² + 4³ + 4⁴ + ... + 4¹⁰¹) - (4 + 4² + 4³ + ... + 4¹⁰⁰)
= 4¹⁰¹ - 4
⇒ 12A = 4.3A = 4.(4¹⁰¹ - 4)
= 4¹⁰² - 4²
⇒ 12A + 4² = 4¹⁰²
Mà 12A + 4² = 4ⁿ
⇒ 4ⁿ = 4¹⁰²
⇒ n = 102

\(n_{Fe}=\dfrac{22,4}{56}=0,4\left(mol\right)\\
pthh:Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
0,4 0,4 0,4
\(V_{H_2}=0,4.22,4=8,96l\\
m_{FeCl_2}=0,4.127=50,8g\\
n_{Fe_2O_3}=\dfrac{14}{160}=0,0875\left(mol\right)\\
pthh:Fe_2O_3+3H_2\underrightarrow{t^o}2Fe+3H_2O\)
\(LTL:\dfrac{0,0875}{1}< \dfrac{0,4}{3}\)
=> H2 dư
\(n_{H_2\left(p\text{ư}\right)}=3n_{Fe_2O_3}=0,2625\left(mol\right)\\
m_{H_2\left(d\right)}=\left(0,4-0,2625\right).2=0,275g\\
n_{Fe}=2n_{Fe_2O_3}=0,175\left(mol\right)\\
m_{Fe}=0,175.56=9,8g\)

Bài 1:
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
DO đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
Xin lỗi ạ. Nhưng mk cần bài 2 ạ , xin lỗi zì đã lm phiền

\(y=\dfrac{sinx-cosx}{sinx+cosx}\Rightarrow y'=\dfrac{\left(sinx-cosx\right)'.\left(sinx+cosx\right)-\left(sinx+cosx\right)'.\left(sinx-cosx\right)}{\left(sinx+cosx\right)^2}\)
Dễ thấy : \(\left(sinx-cosx\right)'=cosx+sinx\)
\(\left(sinx+cosx\right)'=cosx-sinx\)
Suy ra : \(y'=\dfrac{\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}=\dfrac{2}{\left(sinx+cosx\right)^2}\)

Bài 5:
a: Phương trình hoành độ giao điểm là:
\(x^2-2x-m^2-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot\left(-m^2-1\right)\)
\(=4+4m^2+4=4m^2+8>0\)
Vậy: (P) cắt (d) tại hai điểm phân biệt
b: Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-1\end{matrix}\right.\)
Theo đề, ta có: \(x_A^2+x_B^2=14\)
\(\Leftrightarrow4-2\left(-m^2-1\right)=14\)
\(\Leftrightarrow2m^2=8\)
hay \(m\in\left\{2;-2\right\}\)

Chỉ thấy bài 5 với 6:
5.
\(f'\left(x\right)+2f\left(x\right)=0\Leftrightarrow f'\left(x\right)=-2f\left(x\right)\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=-2\)
Lấy nguyên hàm 2 vế:
\(\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int-2dx\Rightarrow ln\left(f\left(x\right)\right)=-2x+C\)
Thay \(x=1\Rightarrow0=-2+C\Rightarrow C=2\)
\(\Rightarrow ln\left(f\left(x\right)\right)=-2x+2\Rightarrow f\left(x\right)=e^{-2x+2}\)
\(\Rightarrow f\left(-1\right)=e^4\)
6.
\(f\left(x\right)+x.f'\left(x\right)=2x+1\)
\(\Leftrightarrow x'.f\left(x\right)+x.f'\left(x\right)=2x+1\)
\(\Leftrightarrow\left[x.f\left(x\right)\right]'=2x+1\)
Lấy nguyên hàm 2 vế:
\(\int\left[x.f\left(x\right)\right]'dx=\int\left(2x+1\right)dx\)
\(\Rightarrow x.f\left(x\right)=x^2+x+C\)
Thay \(x=1\Rightarrow1.f\left(1\right)=1+1+C\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=\dfrac{x^2+x+1}{x}\)
\(\Rightarrow f\left(2\right)=\dfrac{7}{2}\)


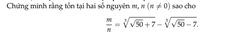
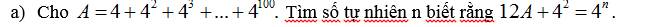 cho mình xin lời giải và công thức bài này với ạ !!!
cho mình xin lời giải và công thức bài này với ạ !!!





\(z=x+yi\Rightarrow w=\dfrac{z}{2+i}=\dfrac{x+yi}{2+i}=\dfrac{\left(x+yi\right)\left(2-i\right)}{4-i^2}=\dfrac{2x+y}{5}+\dfrac{2y-x}{5}i\)
\(\left(1+3i\right)w+1+7i=\left(1+3i\right)\left(\dfrac{2x+y}{5}+\dfrac{2y-x}{5}i\right)+1+7i\)
\(=x-y+1+\left(x+y+7\right)i\)
\(\Rightarrow\left(x-y+1\right)^2+\left(x+y+7\right)^2=50\)
\(\Leftrightarrow x^2+y^2+8x+6y=0\)
Tập hợp z là đường tròn tâm \(I\left(-4;-3\right)\) bán kính \(R=5\)