Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi M a; a + 2 a − 2 thuộc đồ thị hàm số
d ( M;TCD ) = a − 2
d ( M;TCN ) = 4 a − 2
Tổng khoảng cách= a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4
Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0 do hoành độ dương nên a=4
Vậy M(4;3)
Đáp án B
Gọi M a; a + 2 a − 2 thuộc đồ thị hàm số
d ( M;TCD ) = a − 2
d ( M;TCN ) = 4 a − 2
Tổng khoảng cách = a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4
Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0 do hoành độ dương nên a=4
Vậy M(4;3)
Đáp án A
Gọi M a ; 2 a + 2 a − 1 , tiệm cận đứng x = 1 ; tiệm cận ngang y = 2 .
Khi đó d = d M ; T C D + d M ; T C N = a − 1 + 4 a − 1 ≥ 4
Dấu bằng xảy ra ⇔ a − 1 2 = 4 ⇔ a = 3 a = − 1 ⇒ M − 1 ; 0 M 3 ; 4 .
Đáp án A
Đồ thị hàm số y = 2 x + 2 x − 1 C có hai đường tiệm cận là x = 1 d 1 ; y = 2 d 2 .
Gọi M ∈ C ⇒ M m ; 2 m + 2 m − 1 → d M ; d 1 = m − 1 d M ; d 2 = 2 m + 2 m − 1 − 2 = 4 m − 1
Khi đó d M ; d 1 + d M ; d 2 = m − 1 + 4 m − 1 ≥ 2 m − 1 . 4 m − 1 = 4 .
Dấu “=” xảy ra ⇔ m − 1 = 4 m − 1 ⇔ m − 1 2 = 4 ⇔ m = 3 m = − 1 .
Vậy M 3 ; 4 M − 1 ; 0 .
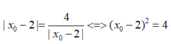
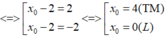
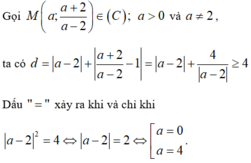
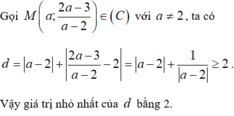
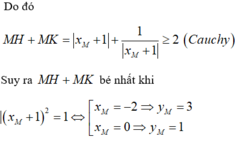
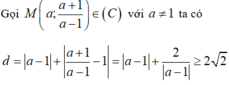
Dễ thấy tiệm cân đứng của \(\left(C\right)\) là \(d_1:x+1=0\), tiệm cân ngang là \(d_2:y-2=0\)
Vì \(M\in\left(C\right)\) nên \(M\left(x_0;\frac{2x_0-1}{x_0+1}\right)\), ta có:
\(d\left(M,d_1\right)=\left|x_0+1\right|;d\left(M,d_2\right)=\left|\frac{2x_0-1}{x_0+1}-2\right|=\left|\frac{-3}{x_0+1}\right|\)
Suy ra \(d\left(M,d_1\right)+d\left(M,d_2\right)=\left|x_0+1\right|+\left|\frac{-3}{x_0+1}\right|\ge2\sqrt{\left|x_0+1\right|.\left|\frac{-3}{x_0+1}\right|}=2\sqrt{3}\)
Đạt được khi \(M\left(\sqrt{3}-1;2-\sqrt{3}\right)\) hoặc \(M\left(-\sqrt{3}-1;2+\sqrt{3}\right)\)