Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giao điểm của đồ thị hàm số (C) và trục tung là điểm N(0;1)
Ta có : \(f'\left(x\right)=\frac{3}{\left(1-x\right)^2}\) suy ra tiếp tuyến tại điểm N là \(\left(\Delta\right):y=3x+1\Leftrightarrow\left(\Delta\right):3x-y+1=0\)
Xét điểm \(M\left(a+1;\frac{2a+3}{-a}\right)\in\left(C\right),a>0\)
Ta có : \(d_{M\\Delta }=\frac{\left|3\left(a+1\right)+\frac{2a+3}{a}+1\right|}{\sqrt{10}}=\frac{1}{\sqrt{10}}.\frac{3a^2+6a}{+3a}=\frac{3}{\sqrt{10}}\left(a+\frac{2}{a}+1\right)\ge\frac{3}{\sqrt{10}}\left(2\sqrt{2}+1\right)\)
Dấu bằng xảy ra khi \(a=\frac{2}{a}\Leftrightarrow a=\sqrt{2}\Rightarrow M\left(\sqrt{2}+1;\frac{2\sqrt{2}+5}{-\sqrt{2}}\right)\)

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

mk nhầm câu c là 25f(x)
câu d là 24f(x)
mk nhầm nũa câu hỏi là cái f(x+2)-f(x) là bỏ nha

Lần sau em đăng bài ở học 24 để mọi người giúp đỡ em nhé!
Link đây: Cộng đồng học tập online | Học trực tuyến
1. Gọi I là tâm của mặt cầu cần tìm
Vì I thuộc d
=> I( a; -1; -a)
Mặt cầu tiếp xúc với hai mặt phẳng (p), (Q). nên ta co:
d(I; (P))=d(I;(Q))
<=> \(\frac{\left|a+2\left(-1\right)+2\left(-a\right)+3\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|a+2\left(-1\right)+2\left(-a\right)+7\right|}{\sqrt{1^2+2^2+2^2}}\)
\(\Leftrightarrow\frac{\left|-a+1\right|}{3}=\frac{\left|-a+5\right|}{3}\Leftrightarrow a=3\)
=> I(3; -1; -3) ; bán kinh : R=d(I; P)=2/3
=> Phương trình mặt cầu:
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
đáp án C.
2. Gọi I là tâm mặt cầu: I(1; -1; 0)
Ta có: Phương trình mặt phẳng (P) tiếp xúc vs mặt Cầu S tại M
=> IM vuông góc vs mặt phẳng (P)
=> \(\overrightarrow{n_p}=\overrightarrow{MI}=\left(1;0;0\right)\)
=> Phương trình mặt phẳng (P) có véc tơ pháp tuyến: \(\overrightarrow{n_p}\)và qua điểm M
1(x-0)+0(y+1)+0(z-0) =0<=> x=0
đáp án B
3.
\(f\left(x\right)=\dfrac{1}{256}\left(2x+3\right)^{10}=\dfrac{1}{256} \sum \limits_{k=0} ^{10}C_{k}^{10}(2x)^k.3^{10-k}\)
Để có hệ số x^8 thì k=8 khi đó hệ số của x^8 là:
\(\dfrac{1}{256}C_{8}^{10}.2^8.3^{10-8}=405\)
đáp án D
4.
pt <=> \(\left(2.5\right)^{x^2-3}=10^{-2}.10^{3x-3}\)
\(\Leftrightarrow10^{x^2-3}=10^{3x-5}\)
\(\Leftrightarrow x^2-3=3x-5\Leftrightarrow x^2-3x+5=0\)
=> theo định lí viet tổng các nghiệm bằng 3, tích các nghiệm bằng 5
Đáp án A

1.
Để ĐTHS có 2 tiệm cận thì \(m\ne-3\)
Khi đó:
\(\lim\limits_{x\rightarrow\infty}\frac{mx-3}{x+1}=m\Rightarrow y=m\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow-1}\frac{mx-3}{x+1}=\infty\Rightarrow x=-1\) là tiệm cận đứng
Giao điểm 2 tiệm cận có tọa độ \(A\left(-1;m\right)\)
Để A thuộc \(y=x+3\Leftrightarrow m=-1+3\Rightarrow m=2\)
2.
\(\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{x-2}}{x^2-4}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow2}\frac{\sqrt{x-2}}{x^2-4}=\infty\Rightarrow x=2\) là 1 TCĐ
\(x=-2\) ko thuộc TXĐ nên ko phải là tiệm cận
Vậy ĐTHS có 2 tiệm cận
3.
Để ĐTHS có đúng 2 TCĐ \(\Leftrightarrow x^2-mx+5=0\) có 2 nghiệm pb khác 1
\(\Leftrightarrow\left\{{}\begin{matrix}6-m\ne0\\\Delta=m^2-20>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne6\\\left[{}\begin{matrix}m\ge2\sqrt{5}\\m\le-2\sqrt{5}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{5;-5\right\}\)
Đề bài sai hoặc đáp án sai

y = 2x2 + 2mx + m -1 (Cm). Đây là hàm số bậc hai, đồ thị là parabol quay bề lõm lên phía trên.
a) m = 1 ⇒ y = 2x2 + 2x
Tập xác định D = R
\(\lim\limits_{x\rightarrow+\infty}y\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty\)
Bảng biến thiên:
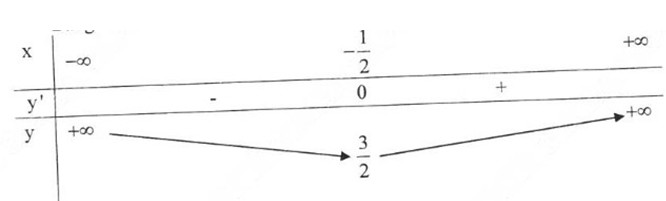
Đồ thị hàm số:
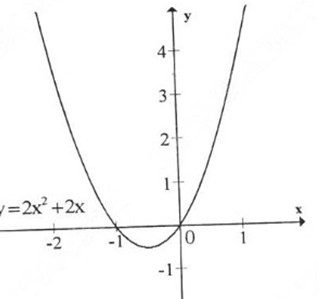
b) Tổng quát y = 2x2 + 2mx + m -1 có tập xác định D = R
y′=4x+2m=0⇔\(x=-\dfrac{m}{2}\).
Suy ra y’ > 0 với \(x>-\dfrac{m}{2}\) và \(y'< 0\) với \(x< -\dfrac{m}{2}\) tức là hàm số nghịch biến trên \(\left(-\infty;\dfrac{-m}{2}\right)\) và đồng biến trên \(\left(-\dfrac{m}{2};+\infty\right)\)
i) Để hàm số đồng biến trên khoảng (-1, +∞) thì phải có điều kiện (−1,+∞)∈(−\(\dfrac{m}{2}\),+∞)
Hay \(-\dfrac{m}{2}< -1\)\(\Leftrightarrow m>2\)
ii) Hàm số đạt cực trị tại \(x=\dfrac{m}{2}\)
Để hàm số đạt cực trị trong khoảng (-1, +∞), ta phải có:
\(-\dfrac{m}{2}\in\left(-1;+\infty\right)\) hay \(-\dfrac{m}{2}>-1\Leftrightarrow m< 2\).
c) (Cm) luôn cắt Ox tại hai điểm phân biệt
⇔ phương trình 2x2 + 2mx + m – 1 = 0 có hai nghiệm phân biệt.
Ta có:
Δ’ = m2 – 2m + 2 = (m-1)2 + 1 > 0 ∀m
Vậy (Cm) luôn cắt O x tại hai điểm phân biệt.

Xét phương trình hoành độ giao điểm của đồ thị (C) và d :
\(\frac{2x+3}{x+2}=-2x+m\)\(\Leftrightarrow\begin{cases}x\ne-2\\2x^2+\left(6-m\right)x+3-2m=0\end{cases}\) (*)
Xét phương trình (*), ta có \(\Delta>0\), mọi \(m\in R\) và x=-2 không là nghiệm của (*) nên d luôn cắt đồ thị (C) tại 2 điểm phân biệt A, B với mọi m
Hệ số góc của tiếp tuyến tại A, tại B lần lượt là :
\(k_1=\frac{1}{\left(x_1+1\right)^2};k_2=\frac{1}{\left(x_2+1\right)^2}\) trong đó \(x_1,x_2\) là 2 nghiệm của phương trình (*)
Ta thấy :
\(k_1.k_2=\frac{1}{\left(x_1+1\right)^2.\left(x_2+1\right)^2}=\frac{1}{\left(x_1x_2+2x_1+2x_2+4\right)^2}=4\) (\(k_1>0;k_2>0\) )
Có \(P=\left(k_1\right)^{2014}+\left(k_2\right)^{2014}\ge2\sqrt{\left(k_1k_2\right)^{2014}}=2^{2015}\)
Do đó , Min \(P=2^{2015}\) đạt được khi và chỉ khi \(k_1=k_2\)
\(\Leftrightarrow\frac{1}{\left(x_1+2\right)^2}=\frac{1}{\left(x_2+2\right)^2}\Leftrightarrow\left(x_1+2\right)^2=\left(x_2+2\right)^2\)
Do \(x_1,x_2\) phân biệt nên ta có \(x_1+2=-x_2-2\)
\(\Leftrightarrow x_1+x_2=-4\Leftrightarrow m=-2\)
Vậy giá trị cần tìm là \(m=-2\)

Đáp án C