Câu rút gọn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 2 2022
Rút gọn CN: Đang đi cùng bố mẹ đến công viên
Đi với ai?
Rút gọn VN: Hôm qua ai cho cậu mượn chiếc bút này?
Mẹ tớ!
Rút gọn cả CN VN Ngày mai
Hôm khác
14 tháng 2 2022
P/s: xin lỗi em, anh quên =)?
Tham khảo: Nằm cạnh chân đồi, chính là quê hương yêu dấu của em. Nơi đây người dân bao đời sinh sống bằng nghề làm nón. Nhìn đâu cũng là màu trắng của những chiếc lá cọ đã được cắt và nhuộm màu. Là những chiếc nón xinh xắn được phơi trên giàn cao. Cùng với đó, là những mảnh vườn rộng xanh mướt các loại rau trái. Có được như thế, chính bởi đức tính chăm chỉ, chịu khó của người dân quê em. Sáng thì ra ruộng, ra vườn, chiều thì hái lá cọ, nhuộm màu, chuốt tre làm khung, tối ngồi may nón. Bận rộn cả ngày, lao động hăng say. Nhờ vậy mà quê hương ngày càng trù phú.
→ Câu rút gọn: Bận rộn cả ngày, lao động hăng say.
UT
14 tháng 2 2022
Tham khảo e nhé!
Tiếng trống trường vang lên rộn rã, báo hiệu giờ ra chơi của chúng em đã đế. Sân trường đang lặng thinh, im ắng bỗng trở nên rộn rã bởi tiếng cười, tiếng nói của các cô cậu học trò. Góc ghế đá sân trường, các bạn nữ ngồi thầm thì nhỏ to với những câu chuyện vui vẻ. Rất nhiều bạn học sinh khác chọn không gian ở căng tin canh sân trường để tranh thủ ăn sáng hoặc cùng ngồi uống nước, nghỉ ngơi sau giờ học căng thẳng. Rộn ràng nhất là góc sân trường, mọi người đang tổ chức rất nhiều trò chơi vui nhộn. Nhảy dây. Kéo co. Chơi bóng rổ. Tất cả tạo nên một bức tranh nhộn nhịp, vui tươi về giờ ra chơi dưới sân trường.
Câu rút gọn: Nhảy dây. Kéo co. Chơi bóng rổ.
HT
giúp mình câu 6,7,8,9,10 v ạ rút gọn ạ
1
DM
8 tháng 8 2021
\(A=\left(\sqrt{2}-8\sqrt{32}+2\sqrt{450}\right):\left(-3\sqrt{8}\right)\)
\(=\left(\sqrt{2}-32\sqrt{2}+30\sqrt{2}\right):\left(-6\sqrt{2}\right)\)
\(=\sqrt{2}\left[\left(1-32+30\right):\left(-6\right)\right]\)
\(=\sqrt{2}\left[\left(-1\right):\left(-6\right)\right]\)
\(=\sqrt{2}.\dfrac{1}{6}\)
\(=\dfrac{\sqrt{2}}{6}\)
2
19 tháng 5 2022
Với `x >= 0,x \ne 1` có:
`C=A/B=A:B=[\sqrt{x}+1]/[x+\sqrt{x}+1]:(\sqrt{x}/[x\sqrt{x}-1]+1/[\sqrt{x}-1])`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1]:[\sqrt{x}+x+\sqrt{x}+1]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[x+2\sqrt{x}+1]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[(\sqrt{x}+1)^2]`
`C=[\sqrt{x}-1]/[\sqrt{x}+1]`
19 tháng 5 2022
1.Thế \(x=4\) vào A, ta được:
\(A=\dfrac{\sqrt{4}+1}{4+\sqrt{4}+1}=\dfrac{2+1}{4+2+1}=\dfrac{3}{7}\)
2.
\(B=\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}^3-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}+\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{A}{B}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}:\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}.\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(C=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
19 tháng 10 2021
\(15,A=\dfrac{x-1-4\sqrt{x}+4+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ A=\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\\ 16,B=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{2\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\\ B=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-2\left(\sqrt{x}+1\right)+2\left(\sqrt{x}+1\right)\\ B=x-\sqrt{x}-2\sqrt{x}-2+2\sqrt{x}+2=x-\sqrt{x}\)
NB
19 tháng 10 2021
15. \(=\dfrac{x-1-4\left(\sqrt{x}-1\right)+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{x-4\sqrt{x}+4}{x-1}.\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\left(\sqrt{x}-2\right)^2.\dfrac{1}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
DA
4
13 tháng 3 2022
cảm ơn bạn nhưng bạn trình bày giúp mình được ko ạ mình cảm ơn:3
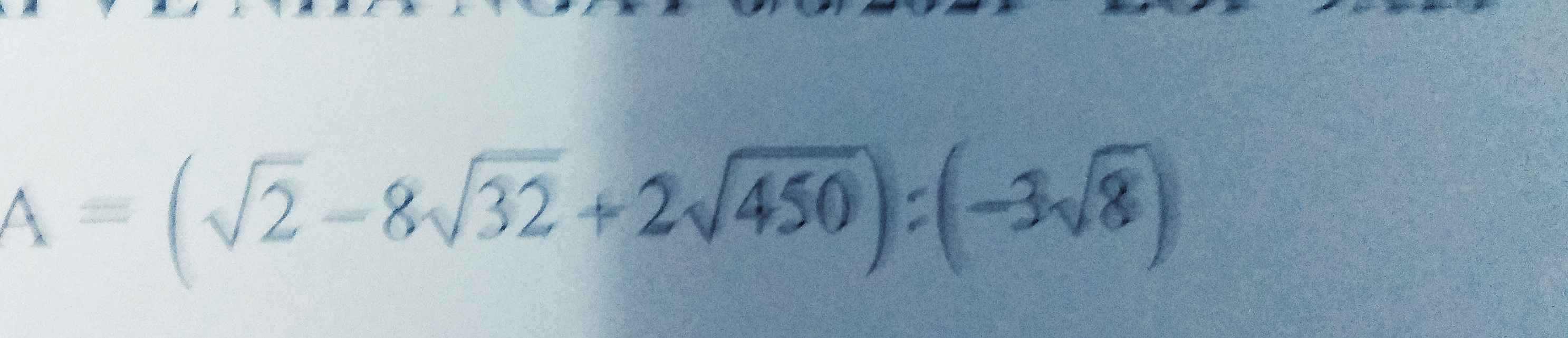
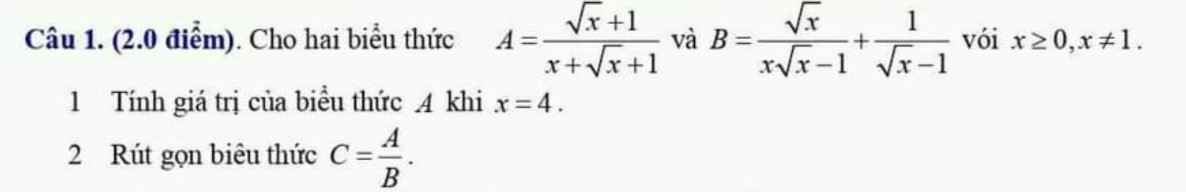
b) Ta có: \(B=\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\)
\(=\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}\)