Giúp mik nha đang cần gấp : Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M, biết AOB=100° . Tính AMB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Yêu cầu của bạn có phải tính góc MAB không?
Nếu có thì sau đây là bài giải!
Giải:
Góc AOM=50o, góc AMO=40o (tam giác AOM vuông tại A).
AB vuông góc với OM (AM và BM là hai tiếp tuyến của (O,OA).
Suy ra, góc MAB+góc AMO=90o \(\Leftrightarrow\) Góc MAB=90o-góc AMO=90o-40o=50o.

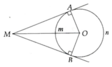
a, Chứng minh được OM là tia phân giác của góc
A
M
B
^
. Từ đó ta tìm được
A
M
O
^
=
20
0
và
A
O
M
^
=
70
0
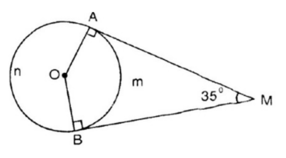
b, sđ A m B ⏜ = A O B ^ = 140 0
=> sđ A n B ⏜ = 220 0

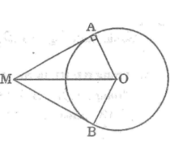
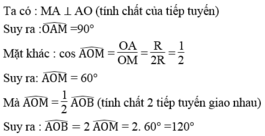
Xét ΔAOM vuông tại A có \(\cos\widehat{OAM}=\dfrac{R}{2R}=\dfrac{1}{2}\)
nên \(\widehat{OAM}=60^0\)(1)
Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: OM là phân giác của góc AOB(2)
Từ (1) và (2) suy ra \(\widehat{AOB}=120^0\)
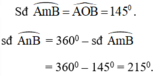

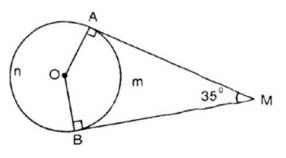
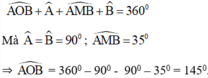

Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AOB}+\widehat{AMB}=360^0\)
=>\(\widehat{AMB}+100^0+90^0+90^0=360^0\)
=>\(\widehat{AMB}=80^0\)