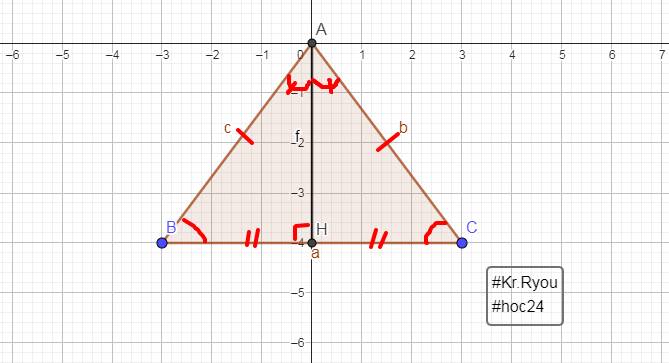
cho tam giác ABC cân tại A , H là trung điểm BC
a) chứng minh tam giác AHB = tam giác AHC
b) chứng minh AH ⊥ BC
c) chứng minh tam giác AEF cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TH
Thanh Hoàng Thanh
17 tháng 3 2022
Đúng(0)
Những câu hỏi liên quan
18 tháng 2 2022
a: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
b: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
c: Ta có: M nằm trên đường trung trực của AC
nên MA=MC
hay ΔMAC cân tại M
29 tháng 10 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của \(\widehat{BAC}\)
c: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=BC/2=3cm
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2+3^2=5^2\)
=>\(HA^2=25-9=16\)
=>HA=4(cm)
7 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC,}` $\widehat {B} = \widehat {C}$
Vì `\text {AH}` là đường cao
`-> \text {AH} \bot \text {BC}`
`->` $\widehat {AHB} = \widehat {AHC} = 90^0$
Xét `2 \Delta` vuông `AHB` và `AHC`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
`=> \Delta AHB = \Delta AHC (ch-gn)`
`b,`
Vì `\Delta AHB = \Delta AHC (a)`
`-> \text {HB = HC (2 cạnh tương ứng)}`
`-> \text {H là trung điểm của BC}`
Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)
Vì `\Delta ABC` cân tại A.
Mà `\text {AH}` là đường cao
`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`
`-> \text {AH cũng là đường trung tuyến}`
`-> \text {H là trung điểm của BC}`
`c,`
Vì `\Delta AHB = \Delta AHC (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$
`-> \text {AH là tia phân giác của} \Delta ABC`
Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)
Vì `\Delta ABC` cân tại A.
Mà `\text {AH}` là đường cao
`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`
`-> \text {AH cũng là đường phân giác}`
7 tháng 6 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
c: ΔABC cân tại A
mà AH là trung tuyến
nên AH là phân giác
31 tháng 12 2021
a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
21 tháng 12 2022
a: Xét ΔHBA vuông tại H và ΔHCA vuông tại H có
AH chung
AB=AC
Do đó: ΔHBA=ΔHCA
b: Xét ΔABM và ΔACM có
AB=AC
góc BAM=góc CAM
AM chung
Do đó: ΔABM=ΔACM
=>góc MAB=góc MAC
c: ΔABM=ΔACM
nên MB=MC