1. Cho tam giác ABC cân A, P là một điểm bất kì thuộc BC. Gọi M,N lần lượt là trung điểm của BP và CP. Đường trung trực của BP cắt AB tại E. Đường trung trực của CP cắt AC tại F.
a) Chứng minh AEPF là hình bình hành
b) PE+DF không đổi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tự vẽ hình nhé
a)tam giác ABC cân tại A(gt)
=>góc ABC=góc ACB
Xét tam giác BEP có: E thuộc đường trung trực của BP
=>BE=EP
=>tam giác BEP cân tại E
=>góc EBP=góc EPB,mà góc EBP=góc ACB (do góc ABC=góc ACB(cmt))
=>góc EPB=góc ACN,mà chúng ở vị trí đồng vị
=>EP//CF hay EP//AF
Xét tam giác CPF có: F thuộc đường trung trực CP=>CF=PF
=>tam giác CPF cân tại F
=>góc FPC=góc FCP,mà ABC=góc FCP(do góc ABC=góc ACB(cmt))
=>góc FPC=góc ABC,mà chúng ở vị trí đồng vị
=>AB//PF hay AE//PF
Xét tứ giác AEPF có: EP//AF (cmt); AE//PF(cmt)
=>tứ giác AEPF là hình bình hành (DHNB.......)
b, AEPF là hình bình hành (cmt)
=>AF=PE
Lại có CF=PF(cmt)
=>PE + PF = AF + CF = AC không phụ thuộc vào vị trí của điểm P trên BC


Ta có tam giác EPQ cân tại E và CQ là phân giác góc BCA, nên E P Q ^ = E Q P ^ = H Q C ^ = 90 0 − H C Q ^ = 90 0 − P C K ^ .
Do đó E P Q ^ + P C K ^ = 90 0 , nên P K ⊥ A C .

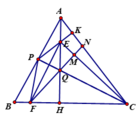
Trong tam giác EFC có C Q ⊥ E F (do EF là trung trực PQ); E Q ⊥ F C nên F Q ⊥ E C .
Từ đó
E
M
N
^
=
90
0
, nên tứ giác EKNM nội tiếp đường tròn đường tròn đường kính ![]() .
.
Ta có tứ giác EKCH nội tiếp đường tròn đường kính EC nên P E Q ^ = H C K ^ .
Chú ý: EF là phân giác góc PEQ và CQ là phân giác góc HCK, do đó P E F ^ = 1 2 P E Q ^ = 1 2 H C K ^ = P C F ^ . Do đó tứ giác PECF nội tiếp.

a: Xét ΔAMO vuông tại M và ΔANO vuông tại N có
AO chung
AM=AN
Do đó: ΔAMO=ΔANO
=>góc MAO=góc NAO
=>AO là phân giác của góc MAN
b: OB=OA
OA=OC
Do đó: OB=OC
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
Một bài toán hay
Bạn tự vẽ hình nhé
Ta có
Góc B = Góc C (tam giác ABC cân tại A) (1)
Tam giác BEP và tam giác FPC lần lượt cân tại E và F Vì có đường trung tuyến và trung trực trùng nhau
=> Góc EPB =Góc EBP : Góc FCP = Góc FPC (2)
Từ (1) và (2)
=> Góc EPB =Góc EBP =Góc FCP = Góc FPC
Thay Góc EPB =Góc EBP = Góc FPC Bằng góc C
+) Góc EPF = 180 độ -(2x Góc C)
+) Góc PFC=180 độ -(2x Goc C)
=> Góc EPf =Góc PFC
=> EP // AF (*)
Góc EAP= 2x Góc C (tc góc ngoài )
Mà Góc EPF+2x Góc C =180 độ
=> Góc EAP +Góc EP=180 đọ
=>AE//PF (**)
Từ (*) và (**) => EAPF là hình bình hành
B sửa lại thành PE+PF nhé
EAPF là hình bình hành => EA=FP
Mặt khác EB=EF
=>EP+FP=EA+EB=AB ( cst)
Chúc bạn hok tốt ^^