cứu tui với tui cần giúp :(((((((((((((((((((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Dãy trên là dãy cách đều với khoảng cách = 8
Số thứ 110 là: $(110-1)\times 8+144=1016$
Tổng của 110 số hạng đầu tiên:
$(1016+144)\times 110:2=63800$

Bài 10:
1: \(\left(\dfrac{5x+y}{x^2-5xy}+\dfrac{5x-y}{x^2+5xy}\right)\cdot\dfrac{x^2-25y^2}{x^2+y^2}\)
\(=\left(\dfrac{5x+y}{x\left(x-5y\right)}+\dfrac{5x-y}{x\left(x+5y\right)}\right)\cdot\dfrac{\left(x-5y\right)\cdot\left(x+5y\right)}{x^2+y^2}\)
\(=\dfrac{\left(5x+y\right)\left(x+5y\right)+\left(5x-y\right)\left(x-5y\right)}{x\left(x-5y\right)\left(x+5y\right)}\cdot\dfrac{\left(x-5y\right)\left(x+5y\right)}{x^2+y^2}\)
\(=\dfrac{5x^2+25xy+xy+5y^2+5x^2-25xy-xy+5y^2}{x\left(x^2+y^2\right)}\)
\(=\dfrac{10x^2+10y^2}{x\left(x^2+y^2\right)}=\dfrac{10\left(x^2+y^2\right)}{x\left(x^2+y^2\right)}=\dfrac{10}{x}\)
2: \(\dfrac{4xy}{y^2-x^2}:\left(\dfrac{1}{x^2+2xy+y^2}-\dfrac{1}{x^2-y^2}\right)\)
\(=\dfrac{-4xy}{\left(x-y\right)\left(x+y\right)}:\left(\dfrac{1}{\left(x+y\right)^2}-\dfrac{1}{\left(x-y\right)\left(x+y\right)}\right)\)
\(=\dfrac{-4xy}{\left(x-y\right)\left(x+y\right)}:\dfrac{x-y-x-y}{\left(x-y\right)\left(x+y\right)^2}\)
\(=\dfrac{-4xy}{\left(x-y\right)\left(x+y\right)}\cdot\dfrac{\left(x-y\right)\left(x+y\right)^2}{-2y}\)
\(=2x\left(x+y\right)\)
Bài 11:
1: ĐKXĐ: \(x\notin\left\{0;3;-3\right\}\)
\(\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{3x+9}\right)\)
\(=\left(\dfrac{9}{x\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x\left(x+3\right)}-\dfrac{x}{3\left(x+3\right)}\right)\)
\(=\dfrac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\dfrac{3\left(x-3\right)-x^2}{3x\left(x+3\right)}\)
\(=\dfrac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}\cdot\dfrac{3x\left(x+3\right)}{-\left(x^2-3x+9\right)}\)
\(=\dfrac{-3}{x-3}\)
2: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\left(\dfrac{2}{x-2}-\dfrac{2}{x+2}\right)\cdot\dfrac{x^2+4x+4}{8}\)
\(=\left(\dfrac{2x+4-2x+4}{\left(x-2\right)\left(x+2\right)}\right)\cdot\dfrac{\left(x+2\right)^2}{8}\)
\(=\dfrac{8\left(x+2\right)^2}{8\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)
3: ĐKXĐ: \(x\notin\left\{\dfrac{1}{3};-\dfrac{1}{3};0;-\dfrac{5}{3}\right\}\)
\(\left(\dfrac{3x}{1-3x}+\dfrac{2x}{3x+1}\right):\dfrac{6x^2+10x}{1-6x+9x^2}\)
\(=\left(\dfrac{-3x}{3x-1}+\dfrac{2x}{3x+1}\right)\cdot\dfrac{\left(3x-1\right)^2}{2x\left(3x+5\right)}\)
\(=\dfrac{-3x\left(3x+1\right)+2x\left(3x-1\right)}{\left(3x-1\right)\left(3x+1\right)}\cdot\dfrac{\left(3x-1\right)^2}{2x\left(3x+5\right)}\)
\(=\dfrac{-9x^2-3x+6x^2-2x}{\left(3x+1\right)}\cdot\dfrac{3x-1}{2x\left(3x+5\right)}\)
\(=\dfrac{-x\left(3x+5\right)}{\left(3x+1\right)}\cdot\dfrac{3x-1}{2x\left(3x+5\right)}=\dfrac{-3x+1}{2\left(3x+1\right)}\)
4: ĐKXĐ: \(x\notin\left\{0;5;-5\right\}\)
\(\left(\dfrac{x}{x^2-25}-\dfrac{x-5}{x^2+5x}\right):\dfrac{2x-5}{x^2+5x}+\dfrac{x}{5-x}\)
\(=\left(\dfrac{x}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{x\left(x+5\right)}\right)\cdot\dfrac{x\left(x+5\right)}{2x-5}+\dfrac{x}{5-x}\)
\(=\dfrac{x^2-\left(x-5\right)^2}{x\left(x-5\right)\left(x+5\right)}\cdot\dfrac{x\left(x+5\right)}{2x-5}-\dfrac{x}{x-5}\)
\(=\dfrac{\left(x-x+5\right)\left(x+x-5\right)}{\left(x-5\right)\left(2x-5\right)}-\dfrac{x}{x-5}\)
\(=\dfrac{5}{x-5}-\dfrac{x}{x-5}=\dfrac{5-x}{x-5}=-1\)

4: Chiều dài thật là: 5,5*100=550cm=5,5m
5:
Sau ngày 3 còn 13:2/3=19,5(m)
Sau ngày 2 còn (19,5+9):0,75=38(m)
Sau ngày 1 còn (38+10):0,8=60(m)
Ban đầu có (60+5):5/6=78(m)
1:
Số tiền 1 cây bút đỏ là 3000*2=6000(đồng)
Số tiền phải trả là:
25*3000*0,95+15*6000*0,9=152250 đồng

Bài 1:
\(a,x^2-y^2-2x+2y=\left(x-y\right)\left(x+y\right)-2\left(x-y\right)=\left(x-y\right)\left(x+y-2\right)\)
\(b,2x+2y-x^2-xy=2\left(x+y\right)-x\left(x+y\right)=\left(2-x\right)\left(x+y\right)\)
\(c,3a^2-6ab+3b^2-12c^2=3\left(a-b\right)^2-12c^2=3\left[\left(a-b\right)^2-4c^2\right]=3\left(a-b-2c\right)\left(a-b+2c\right)\)
\(d,x^2-25+y^2+2xy=\left(x-y\right)^2-25=\left(x-y-5\right)\left(x-y+5\right)\)
Bài 1:
\(e,a^2+2ab+b^2-ac-bc=\left(a+b\right)^2-c\left(a+b\right)=\left(a+b-c\right)\left(a+b\right)\)
\(f,x^2-2x-4y^2-4y=\left(x-1\right)^2-\left(2y+1\right)^2=\left(x-2y-2\right)\left(x+2y\right)\)
\(g,x^2y-x^3-9y+9x=x^2\left(y-x\right)-9\left(y-x\right)=\left(x-3\right)\left(x+3\right)\left(y-x\right)\)
\(h,x^2\left(x-1\right)+16\left(1-x\right)=\left(x-1\right)\left(x-4\right)\left(x+4\right)\)

1) \(\left(x+\dfrac{1}{3}\right)^3=x^3+3.x^2.\dfrac{1}{3}+3.x.\left(\dfrac{1}{3}\right)^2+\left(\dfrac{1}{3}\right)^3\)
\(=x^3+x^2+\dfrac{x}{3}+\dfrac{1}{27}\)
2) \(\left(2x+y^2\right)^3=\left(2x\right)^3+3.\left(2x\right)^2.y^2+3.2x.\left(y^2\right)^2+\left(y^2\right)^3\)
\(=8x^3+12x^2y^2+6xy^4+y^6\)
3) \(\left(\dfrac{1}{2}x^2+\dfrac{1}{3}y\right)^3=\left(\dfrac{1}{2}x^2\right)^3+3.\left(\dfrac{1}{2}x^2\right)^2.\dfrac{1}{3}y+3.\dfrac{1}{2}x^2.\left(\dfrac{1}{3}y\right)^2+\left(\dfrac{1}{3}y\right)^3\)
\(=\dfrac{1}{8}x^6+\dfrac{1}{4}x^4y+\dfrac{1}{6}x^2y^2+\dfrac{1}{27}y^3\)
4) \(\left(3x^2-2y\right)^3=\left(3x^2\right)^3-3.\left(3x^2\right)^2.2y+3.3x^2.\left(2y\right)^2-\left(2y\right)^3\)
\(=27x^6-54x^4y+36x^2y^2-8y^3\)
5) \(\left(\dfrac{2}{3}x^2-\dfrac{1}{2}y\right)^3=\left(\dfrac{2}{3}x^2\right)^3-3.\left(\dfrac{2}{3}x^2\right)^2.\dfrac{1}{2}y+3.\dfrac{2}{3}x^2.\left(\dfrac{1}{2}y\right)^2-\left(\dfrac{1}{2}y\right)^3\)
\(=\dfrac{8}{27}x^6-\dfrac{1}{3}x^4y+\dfrac{1}{2}x^2y^2-\dfrac{1}{8}y^3\)
6) \(\left(2x+\dfrac{1}{2}\right)^3=\left(2x\right)^3+3.\left(2x\right)^2.\dfrac{1}{2}+3.2x.\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3\)
\(=8x^3+6x^2+\dfrac{3}{2}x+\dfrac{1}{8}\)
7) \(\left(x-3\right)^3=x^3-3.x^2.3+3.x.3^2-3^3\)
\(=x^3-9x^2+27x-27\)
8) \(\left(x+1\right)\left(x^2-x+1\right)\)
\(=\left(x+1\right)\left(x^2-x.1+1^2\right)\)
\(=x^3+1^3\)
\(=x+1\)
9) \(\left(x-3\right)\left(x^2+3x+9\right)\)
\(=\left(x-3\right)\left(x^2+x.3+3^2\right)\)
\(=x^3-3^3\)
\(=x^3-27\)
10) \(\left(x-2\right)\left(x^2+2x+4\right)\)
\(=\left(x-2\right)\left(x^2+x.2+2^2\right)\)
\(=x^3-2^3\)
\(=x^3-8\)
11) \(\left(x+4\right)\left(x^2-4x+16\right)\)
\(=\left(x+4\right)\left(x^2-x.4+4^2\right)\)
\(=x^3+4^3\)
\(=x^3+64\)
12) \(\left(x-3y\right)\left(x^2+3xy+9y^2\right)\)
\(=\left(x-3y\right)\left[x^2+x.3y+\left(3y\right)^2\right]\)
\(=x^3-\left(3y\right)^3\)
\(=x^3-27y^3\)
13) \(\left(x^2-\dfrac{1}{3}\right)\left(x^4+\dfrac{1}{3}x^2+\dfrac{1}{9}\right)\)
\(=\left(x^2-\dfrac{1}{3}\right)\left[\left(x^2\right)^2+x^2.\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2\right]\)
\(=\left(x^2\right)^3-\left(\dfrac{1}{3}\right)^3\)
\(=x^6-\dfrac{1}{27}\)
14) \(\left(\dfrac{1}{3}x+2y\right)\left(\dfrac{1}{9}x^2-\dfrac{2}{3}xy+4y^2\right)\)
\(=\left(\dfrac{1}{3}x+2y\right)\left[\left(\dfrac{1}{3}x\right)^2-\dfrac{1}{3}x.2y+\left(2y\right)^2\right]\)
\(=\left(\dfrac{1}{3}x\right)^3+\left(2y\right)^3\)
\(=\dfrac{1}{27}x^3+8y^3\)

1. PTBĐ: Tự sự
2. TTV tự nhiên: con kiến, chiếc lá, bờ
3. Hình ảnh vết nứt ẩn dụ cho những khó khăn, thử thách trong cuộc sống mà chúng ta đối mặt hằng ngày.
4.
Em tham khảo:
Trong cuộc sống, con người cũng phải trải qua những khó khăn, thử thách như “vết nứt” mà con kiến bé nhỏ kia gặp phải. Điều quan trọng là trước khó khăn đó, con người ứng xử và vượt qua khó khăn như thế nào. Hình ảnh con kiến đã cho chúng ta một bài học, hãy biến những trở ngại, khó khăn của ngày hôm nay thành trải nghiệm, là hành trang quý giá cho ngày mai để đạt đến thành công, tươi sáng. Ý kiến cũng tác giả cũng gián tiếp lên tiếng trước một thực trạng, trong cuộc sống, trước những khó khăn, nhiều người còn bi quan, chán nản, bỏ cuộc… đó là thái độ cần thay đổi để vươn lên trong cuộc sống.


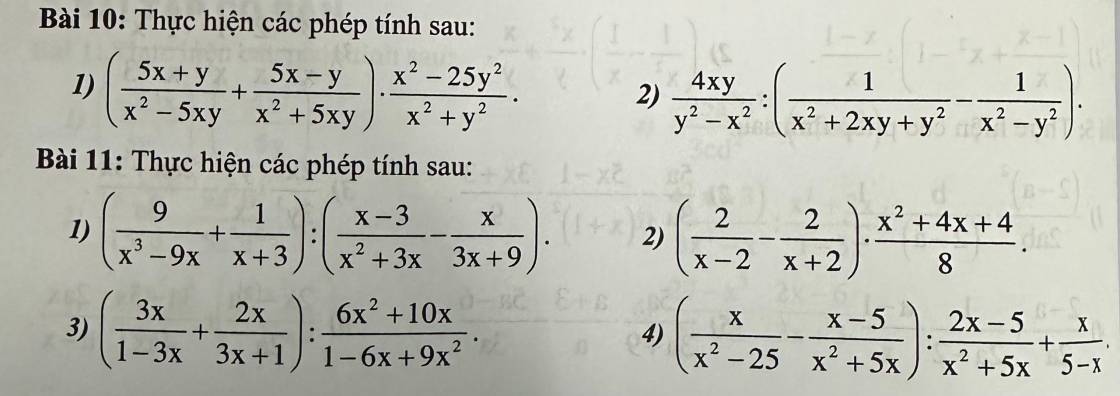

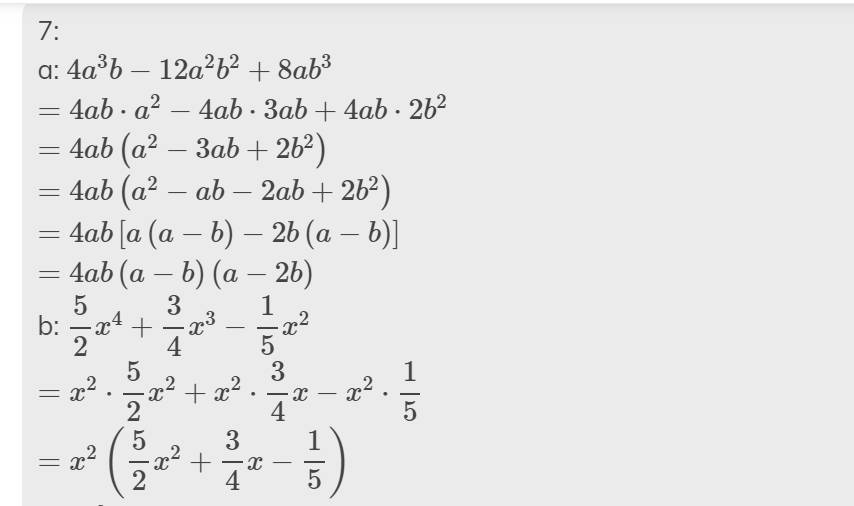
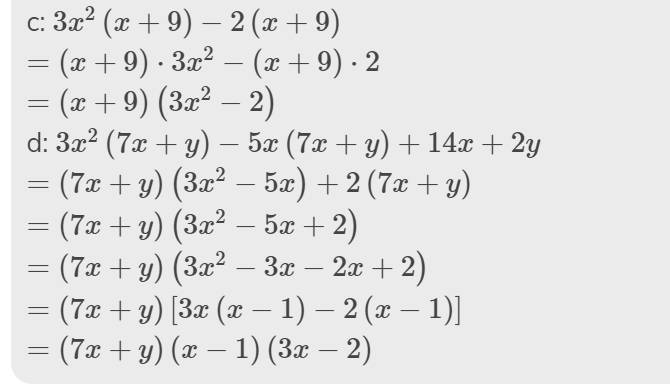
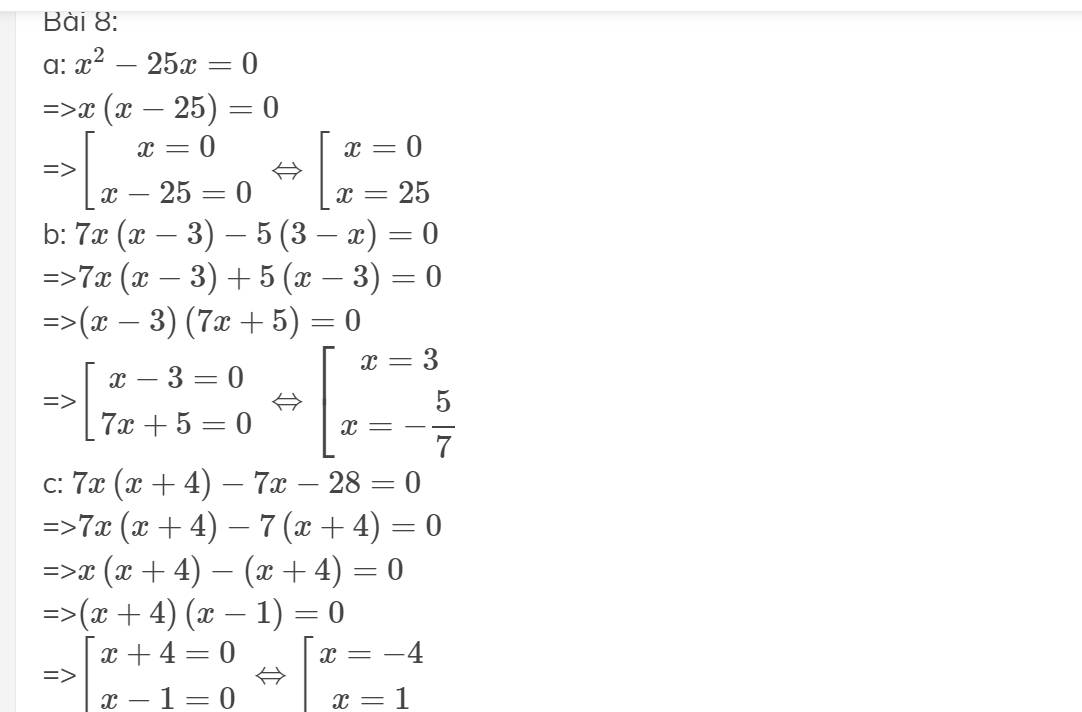
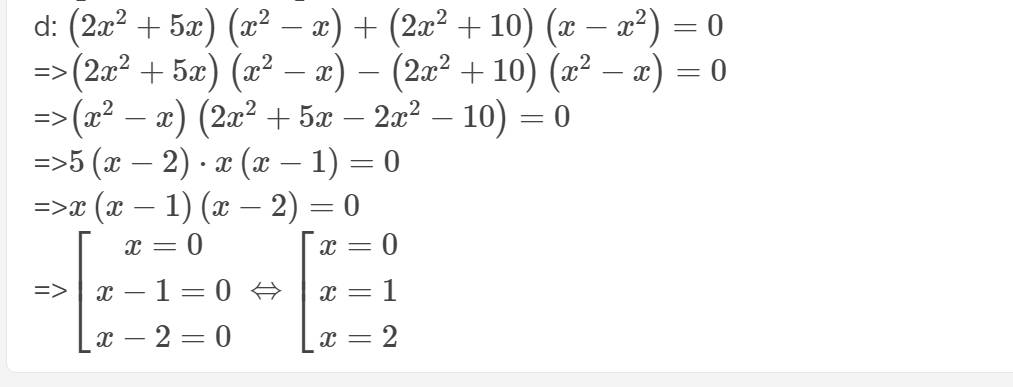

 giúp tui với tui đang cần gấp ạ xong tui tick
giúp tui với tui đang cần gấp ạ xong tui tick Tui đang cần gấp ai giúp tui với xogn tui tick
Tui đang cần gấp ai giúp tui với xogn tui tick 
