Khi chia đa thức 2x4 + 8x3 – 7x2 + 8x – 12 cho x – 2 ta được thương là đa thức Q(x) có bậc là 3. Hãy tìm hệ số của x2 trong Q(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
P + Q = (-5x4 +3x3 + 7x2 + x – 3) + (5x4 – 4x3 – x2 + 3x + 3)
= -5x4 +3x3 + 7x2 + x – 3 + 5x4 – 4x3 – x2 + 3x + 3
= (-5x4 + 5x4 ) + (3x3 – 4x3 ) + (7x2 – x2 ) + (x + 3x) + (-3 + 3)
= 0 + (-x3) + 6x2 +4x
= -x3 + 6x2 +4x
P – Q = (-5x4 +3x3 + 7x2 + x – 3) - (5x4 – 4x3 – x2 + 3x + 3)
= -5x4 +3x3 + 7x2 + x – 3 - 5x4 + 4x3 + x2 - 3x - 3
= (-5x4 - 5x4 ) + (3x3 + 4x3 ) + (7x2 + x2 ) + (x - 3x) + (-3 - 3)
= -10x4 + 7x3 + 8x2 + (-2x) + (-6)
= -10x4 + 7x3 + 8x2 – 2x – 6
a) Đa thức P + Q có bậc là 3
Đa thức P – Q có bậc là 4
b) +) Tại x = 1 thì P + Q = - 13 + 6. 12 + 4.1 = 9
P – Q = -10. 14 + 7.13 + 8.12 – 2. 1 – 6 = -3
+) Tại x = - 1 thì P + Q = - (-1)3 + 6. (-1)2 + 4.(-1) = -(-1) + 6.1 - 4 = 3
P – Q = -10. (-1)4 + 7.(-1)3 + 8.(-1)2 – 2. (-1) – 6 = -10 . 1 + 7.(-1) + 8 + 2 – 6 = -13
c) Đa thức P + Q có nghiệm là x = 0 vì đa thức này có hệ số tự do bằng 0.
CM
23 tháng 9 2019
Sắp xếp lại các hạng tử của Q(x) ta có :
Q(x) = –3x5 + x4 + 3x3 – 2x + 6.
Đặt và thực hiện các phép tính P(x) – Q(x) và Q(x) – P(x), ta có
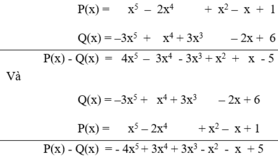
Nhận xét : Các hệ số tương ứng của P(x) – Q(x) và Q(x) - P(x) đối nhau.
Chú ý : Ta gọi hai đa thức có các hệ số tương ứng đối nhau là đa thức đối nhau.
7 tháng 12 2019
a) \(8x^3-18x^2+x+6\)
\(=8x^3-16x^2-2x^2+4x-3x+6\)
\(=8x^2\left(x-2\right)-2x\left(x-2\right)-3\left(x-2\right)\)
\(=\left(x-2\right)\left(8x^2-2x-3\right)\)
\(=\left(x-2\right)\left(8x^2-6x+4x-3\right)\)
\(=\left(x-2\right)\left[2x\left(4x-3\right)+\left(4x-3\right)\right]\)
\(=\left(x-2\right)\left(2x+1\right)\left(4x-3\right)\)
=> g(x) có 3 nghiệm là
x-2=0 <=> x=2
2x+1=0 <=> x=-1/2
4x-3=0 <=> x=3/4
vậy đa thức g(x) có nghiệm là x={2;-1/2;3/4}
b) tự làm đi (mk ko bt làm)
17 tháng 4 2023
a: A(x)=-x^3+7x^2+2x-15
b: Bậc 3
c: Hệ số cao nhất là -1
Hệ số tự do là -15
d: A(x)+B(x)
=-x^3+7x^2+2x-15+4x^3-x^2+5x-15
=3x^3+6x^2+7x-30
; Q(x) tại x = 1.
11 tháng 5 2022
a, \(P\left(x\right)=5x^2-3x+7\)
\(Q\left(x\right)=-5x^3-x^2+4x-5\)
b, Thay x = 1 vào Q(x) ta được
-5 - 1 + 4 - 5 = -7
c, \(Q\left(x\right)+P\left(x\right)=-5x^3+4x^2+x+2\)
\(Q\left(x\right)-P\left(x\right)=-5x^3-6x^2+7x-12\)
\(-5x^3+9x^2+x=0\Leftrightarrow x\left(-5x^2+9x+1\right)=0\Leftrightarrow x=0;x=\dfrac{9\pm\sqrt{101}}{10}\)
1 tháng 9 2018
1)
Đặt \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e.\)( a khác 0 )
Ta có:
\(f\left(1\right)=a+b+c+d+e=0\) (1)
\(f\left(2\right)=16a+8b+4c+2d+e=0\) (2)
\(f\left(3\right)=81a+27b+9c+3d+e=0\) (3)
\(f\left(4\right)=256a+64b+16c+4d+e=6\) (4)
\(f\left(5\right)=625a+125b+25c+5d+e=72\) (5)
\(A=f\left(2\right)-f\left(1\right)=15a+7b+3c+d=0\)
\(B=f\left(3\right)-f\left(2\right)=65a+19b+5c+d=0\)
\(C=f\left(4\right)-f\left(3\right)=175a+37b+7c+d=6\)
\(D=f\left(5\right)-f\left(4\right)=369a+61b+9c+d=72-6=66\)
\(E=B-A=50a+12b+2c=0\)
\(F=C-B=110a+18b+2c=6\)
\(G=D-C=194a+24b+2c=66-6=60\)
Tiếp tục lấy H=F-E; K=G-F; M=H-K
Ta tìm được a
Thay vào tìm được b,c,d,e
2 tháng 9 2018
1. gọi đa thức cần tìm là f(x) =a.x^4+b.x^3+c.x^2+dx+e
có f(1)=f(2)=f(3) = 0 nên x=1,2,3 la nghiệm của f(x) = 0 vậy f(x) có thể viết dưới dạng f(x) = (x-1)(x-2)(x-3)(mx+n)
thay f(4)=6 và f(5)=72 tìm được m =2 và n= -7
Vậy đa thức f(x) =(x-1)(x-2)(x-3)(2x-7) => e = (-1).(-2).(-3).(-7) = 42
Với x=2010 thì (a 2010^4+b.2010^3+c.2010^2+d.2010 ) luôn chia hết 10 vậy số dư f(2010) chia 10 = số dư d/10 = 2 (42 chia 10 dư 2).
2. Thiếu dữ liệu
3. đa thức f(x) chia đa thức (x-3) có số dư là 2 =>bậc f(x) = bậc (x-3)=1 và f(x) = m.(x-3) +2=mx+2-3m (1)
...........................................(x+4)...................9..........................................f(x) = n(x+4) + 9=nx+4n+9 (2)
để (1)(2) cùng xảy ra thì m=n và (2-3m)=(4n+9) => m = n = -1 khi đó đa thức f(x) = -x +5
Không hiếu dữ liệu cuối f(x) chia 1 đa thức bậc 2 lại có thương là 1 đa thức bậc 2? => vô lý