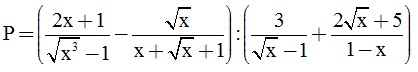
Câu 2.Cho biểu thức: a) Rút gọn biểu thức P.b) Tính giá trị của P khi 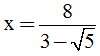.c) Tìm x để P có giá trị là số tự...
Đọc tiếp
Câu 2.Cho biểu thức:
a) Rút gọn biểu thức P.
b) Tính giá trị của P khi 
.
c) Tìm x để P có giá trị là số tự nhiên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
nhận giá trị là số nguyên.
20 tháng 7 2021
a) Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)-2\sqrt{x}-1+2\left(\sqrt{x}+1\right)\)
\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=x-\sqrt{x}+1\)
(Với x > 0; x 1; x4)
11 tháng 1 2023
a: Khi x=64 thì \(A=\dfrac{3\cdot8+1}{8+2}=\dfrac{25}{10}=\dfrac{5}{2}\)
b: \(B=\dfrac{2\sqrt{x}-4-\sqrt{x}+5}{x-4}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}+2}\)
để 
nhận giá trị nguyên
với 
Tìm tất cả các số tự nhiên 
để 
là số nguyên tố.
NL
20 tháng 2 2021
Câu 1:
a) \(A=\left[\dfrac{2}{3x}-\dfrac{2}{x+1}.\left(\dfrac{x+1}{3x}-x-1\right)\right]:\dfrac{x-1}{x}\)
\(=\left[\dfrac{2}{3x}-\dfrac{2}{3x}+\dfrac{2x}{x+1}+\dfrac{2}{x+1}\right]\dfrac{x}{x-1}\)
\(=\left[\dfrac{2x}{x+1}+\dfrac{2}{x+1}\right]\dfrac{x}{x-1}\)
\(=\dfrac{2x+2}{x+1}.\dfrac{x}{x-1}\)
\(=\dfrac{2\left(x+1\right)}{x+1}.\dfrac{x}{x-1}\)
\(=2.\dfrac{x}{x-1}\)
\(=\dfrac{2x}{x-1}\)
20 tháng 2 2021
Câu 1:
ĐKXĐ: \(x\notin\left\{0;-1;1\right\}\)
a) Ta có: \(A=\left(\dfrac{2}{3x}-\dfrac{2}{x+1}\cdot\left(\dfrac{x+1}{3x}-x-1\right)\right):\dfrac{x-1}{x}\)
\(=\left(\dfrac{2}{3x}-\dfrac{2}{x+1}\cdot\left(\dfrac{x+1}{3x}-\dfrac{3x\left(x+1\right)}{3x}\right)\right):\dfrac{x-1}{x}\)
\(=\left(\dfrac{2}{3x}-\dfrac{2}{x+1}\cdot\dfrac{x+1-3x^2-3x}{3x}\right):\dfrac{x-1}{x}\)
\(=\left(\dfrac{2}{3x}-\dfrac{2}{x+1}\cdot\dfrac{-3x^2-2x+1}{3x}\right):\dfrac{x-1}{x}\)
\(=\left(\dfrac{2\left(x+1\right)}{3x\left(x+1\right)}-\dfrac{2\cdot\left(-3x^2-2x+1\right)}{3x\left(x+1\right)}\right):\dfrac{x-1}{x}\)
\(=\dfrac{2x+2+6x^2+4x-2}{3x\left(x+1\right)}:\dfrac{x-1}{x}\)
\(=\dfrac{6x^2+6x}{3x\left(x+1\right)}:\dfrac{x-1}{x}\)
\(=\dfrac{6x\left(x+1\right)}{3x\left(x+1\right)}:\dfrac{x-1}{x}\)
\(=2\cdot\dfrac{x}{x-1}=\dfrac{2x}{x-1}\)
b) Để A nguyên thì \(2x⋮x-1\)
\(\Leftrightarrow2x-2+2⋮x-1\)
mà \(2x-2⋮x-1\)
nên \(2⋮x-1\)
\(\Leftrightarrow x-1\inƯ\left(2\right)\)
\(\Leftrightarrow x-1\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow x\in\left\{2;0;3;-1\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{2;3\right\}\)
Vậy: Để A nguyên thì \(x\in\left\{2;3\right\}\)
N
11 tháng 12 2018
để A xác định
\(\Rightarrow\hept{\begin{cases}x+2\ne0\\x-2\ne0\\x^2\ne4\end{cases}}\Rightarrow x\ne\pm2\)
\(A=\frac{4}{x+2}+\frac{3}{x-2}-\frac{5x-6}{x^2-4}\)
\(A=\frac{4.x-8}{\left(x+2\right).\left(x-2\right)}+\frac{3.x+6}{\left(x-2\right).\left(x+2\right)}-\frac{5x-6}{\left(x-2\right).\left(x+2\right)}\)
\(A=\frac{4x-8+3x+6-5x+6}{\left(x+2\right).\left(x-2\right)}=\frac{2.\left(x+2\right)}{\left(x+2\right).\left(x-2\right)}=\frac{2}{x-2}\)
S
11 tháng 12 2018
\(\frac{4}{x+2}+\frac{3}{x-2}-\frac{5x-6}{x^2-4}=\frac{4}{x+2}+\frac{3}{x-2}-\frac{5x-6}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{4x-8}{\left(x+2\right)\left(x-2\right)}+\frac{3x+4}{\left(x-2\right)\left(x+2\right)}-\frac{5x-6}{\left(x-2\right)\left(x+2\right)}=\frac{4x-8+3x+4-5x+6}{\left(x+2\right)\left(x-2\right)}\)
\(=\frac{2x+2}{\left(x+2\right)\left(x-2\right)}=\frac{2x+2}{x^2-4}\)
C, \(x=4\Rightarrow A=\frac{2x+2}{x^2-4}=\frac{-6}{12}=\frac{-1}{2}\)
d, \(A\inℤ\Leftrightarrow2x+2⋮x^2-4\Leftrightarrow2x^2+2x-2x^2+8⋮x^2-4\Leftrightarrow2x+8⋮x^2-4\)
\(\Leftrightarrow2x^2+8x⋮x^2-4\Leftrightarrow16⋮x^2-4\)
\(x^2-4\inℕ\)
\(\Rightarrow x^2\in\left\{0;4;12\right\}\)
Thử lại thì 12 ko là số chính phương vậy x=0 hoặc x=2 thỏa mãn
mk học lớp 6 mong mn thông cảm nếu có sai sót
29 tháng 12 2021
a: \(A=\dfrac{x^2-2x+2x^2+4x-3x^2-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2}{x+2}\)
5 tháng 1 2023
a, \(\dfrac{x}{x+2}\) + \(\dfrac{2x}{x-2}\) -\(\dfrac{3x^2-4}{x^2-4}\)
= \(\dfrac{x}{x+2}+\dfrac{2x}{x-2}-\dfrac{3x^2+4}{x^2-4}\)
= \(\dfrac{x}{x+2}+\dfrac{2x}{x-2}-\dfrac{3x^2+4}{\left(x+2\right)\left(x-2\right)}\)
= \(\dfrac{x\left(x-2\right)+2x\left(x+2\right)-3x^2-4}{\left(x+2\right)\left(x-2\right)}\)
= \(\dfrac{2x-4}{\left(x+2\right)\left(x-2\right)}=\dfrac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{2}{x+2}\)
Có vài bước mình làm tắc á nha :>
\(P=\left(\frac{2x+1}{\sqrt{x^3}-1}-\frac{\sqrt{x}}{x+\sqrt{x}+1}\right):\left(\frac{3}{\sqrt{x}-1}+\frac{2\sqrt{x}+5}{1-x}\right)\)
\(ĐKXĐ:x\ge0,x\ne1\)
\(P=\frac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\frac{\left(\sqrt{x}+1\right)-\left(2\sqrt{x}+5\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\frac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-2}=\frac{\sqrt{x}+1}{\sqrt{x}-2}\)
b, \(x=\frac{8}{3-\sqrt{5}}=\frac{2\left(9-5\right)}{3-\sqrt{5}}=2\left(3+\sqrt{5}\right)\)
\(=5+2\sqrt{5}+1=\left(\sqrt{5}+1\right)^2\Rightarrow\sqrt{x}=\sqrt{5}+1\)
\(\Rightarrow P=\frac{\sqrt{5}+1+1}{\sqrt{5}+1-2}=\frac{\sqrt{5}+2}{\sqrt{5}-1}\)
c, \(P=\frac{\sqrt{x}-2+3}{\sqrt{x}-2}=1+\frac{3}{\sqrt{x}-2}\in N\)\(\Rightarrow\frac{3}{\sqrt{x}-2}\in Z\)
\(\Rightarrow\sqrt{x}-2\inƯ\left(3\right)\)
\(\Rightarrow x\in\left\{9;25\right\}\)