Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\sqrt{x-2}\)có nghĩa khi\(\sqrt{x-2}\ge0\)
\(\Rightarrow x\ge2\)
\(b,\frac{1}{\sqrt{2x-1}}\)có nghĩa khi \(\sqrt{2x-1}>0\)
\(\Rightarrow2x>1\)
\(\Rightarrow x>\frac{1}{2}\)

a)\(\sqrt{81}-\sqrt{80}\)\(.\sqrt{0,2}\)\(=\sqrt{9^2}-\sqrt{80.0,2}\)\(=9-\sqrt{16}\)\(=9-4=5\)
\(\sqrt{\left(2-\sqrt{5}\right)^2}\)\(-\frac{1}{2}.\sqrt{20}\)\(=|2-\sqrt{5}|-\frac{1}{2}.\sqrt{4.5}\)\(=2-\sqrt{5}-\frac{1}{2}.2\sqrt{5}\)
\(=2-\sqrt{5}-\sqrt{5}=2\)
Tôi lm đc đến đây thôi(@_@)
\(\)

Bài 4 :
a, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=16\Rightarrow AB=4\)cm
Theo định lí Ptago : \(AC=\sqrt{BC^2-AB^2}=\sqrt{64-16}=4\sqrt{3}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{16\sqrt{3}}{8}=2\sqrt{3}\)cm
b, Xét tam giác ABK vuông tại A, đường cao AD
\(AB^2=BD.BK\)( hệ thức lượng ) (1)
Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2=BH.BC\)( hệ thức lượng ) (2)
Từ (1) ; (2) => \(BD.BK=BH.BC\)(3)
c, Xét tam giác BHD và tam giác BKC
^B _ chung
(3) => \(BD.BK=BH.BC\Rightarrow\frac{BD}{BC}=\frac{BH}{BK}\)
Vậy tam giác BHD ~ tam giác BKC ( c.g.c )
=> \(\frac{S_{BHD}}{S_{BKC}}=\left(\frac{BD}{BC}\right)^2\)(4)
Ta có : cosABD = \(\frac{DB}{AB}\)
=> cos2ABD = \(\left(\frac{DB}{AB}\right)^2\)=> cos2ABD = \(\frac{DB^2}{AB^2}=\frac{DB^2}{16}\)
=> \(\frac{1}{4}cos^2\widehat{ABD}=\frac{DB^2}{64}=\frac{DB^2}{8^2}=\frac{DB^2}{BC^2}=\left(\frac{DB}{BC}\right)^2\)
\(\Rightarrow\frac{1}{4}cos^2\widehat{ABD}=\frac{S_{BHD}}{S_{BKC}}\)theo (4)
=> \(S_{BHD}=S_{BKC}.\frac{1}{4}cos^2\widehat{ABD}\)
Bài 3 :
a, Với \(x>0;x\ne1\)
\(A=\left(\frac{1}{x+2\sqrt{x}}-\frac{1}{\sqrt{x}+2}\right):\frac{1-\sqrt{x}}{x+4\sqrt{x}+4}\)
\(=\left(\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right):\frac{1-\sqrt{x}}{\left(\sqrt{x}+2\right)^2}=\frac{\sqrt{x}+2}{\sqrt{x}}\)
b, Ta có : \(A=\frac{5}{3}\Rightarrow\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{3}\Rightarrow3\sqrt{x}+6=5\sqrt{x}\Leftrightarrow6=2\sqrt{x}\Leftrightarrow x=9\)


\(B=\frac{1}{\sqrt{16}-2}-\frac{\sqrt{16}}{4-16}\)
\(B=\frac{1}{4-2}-\frac{4}{-12}\)
\(B=\frac{1}{2}+\frac{1}{3}\)
\(B=\frac{5}{6}\)
\(II\)
\(1,\)số xe công ty dự định là x
số xe thực tế x-2
số tấn mỗi xe chở dự định là \(\frac{24}{x}\)
số tấn mỗi xe thực tế chở là \(\frac{24}{x-2}\)
\(\frac{24}{x-2}-\frac{24}{x}=2\)
\(24x-24x+48=2x\left(x-2\right)\)
\(48=2x^2-4x\)
\(2x^2-4x-48=0\)
\(a=2,b=-4,c=-48\)
\(\Delta=\left(b\right)^2-4ac=16-\left(-384\right)\)
\(\Delta=16+384=400>0\)<=> có 2no pt
\(\sqrt{\Delta}=\sqrt{400}=20\)
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{24}{4}=6\left(tm\right)\)
\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{4-20}{4}=-4\left(ktm\right)\)
\(III\)
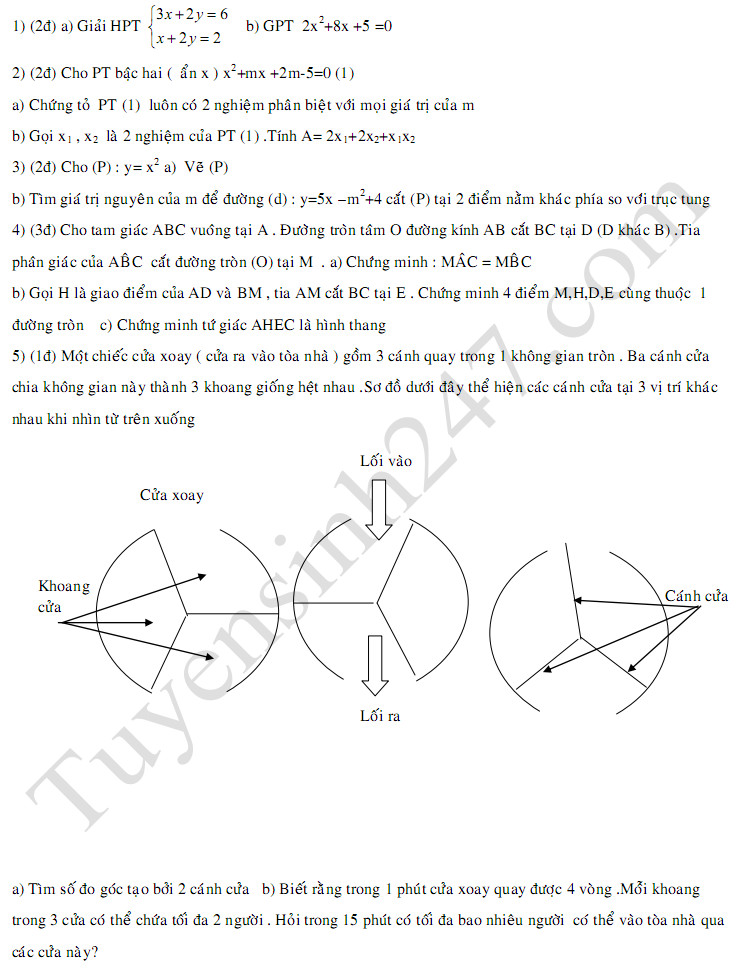
\(1,\hept{\begin{cases}2\left(x+y\right)+\sqrt{x+1}=4\\\left(x+y\right)-3\sqrt{x+1}=-5\end{cases}< =>\hept{\begin{cases}2\left(x+y\right)+\sqrt{x+1}=4\\2\left(x+y\right)-6\sqrt{x+1}=-10\end{cases}}}\)
\(7\sqrt{x+1}=14\)
\(\sqrt{x+1}=2\)
\(\sqrt{x+1}=\sqrt{4}\)
\(x+1=4\)
\(x=3\)
\(2\left(3+y\right)+\sqrt{3+1}=4\)
\(\hept{\begin{cases}x=3\\6+2y+2=4\end{cases}< =>\hept{\begin{cases}x=3\\2y=-4\end{cases}< =>\hept{\begin{cases}x=3\\y=-2\end{cases}}}}\)
\(\)


Hình a/
Áp dụng định lý Pitago:
$x+y=\sqrt{6^2+8^2}=10$
Áp dụng hệ thức lượng trong tam giác vuông:
$6^2=x(x+y)=10x\Rightarrow x=3,6$
$8^2=y(y+x)=10y\Rightarrow y=6,4$
Hình b/
Áp dụng hệ thức lượng trong tam giác vuông:
$12^2=x(x+y)=20x$
$\Rightarrow x=\frac{12^2}{20}=7,2$
$y=20-x=20-7,2=12,8$
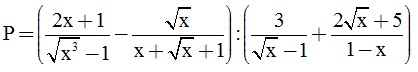
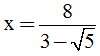 .
.![[Năm 2021] Đề thi Giữa kì 1 Toán lớp 9 có đáp án (10 đề)](https://vietjack.com/de-kiem-tra-lop-9/images/de-thi-giua-ki-1-toan-lop-9-co-dap-an-2021-24855.png)

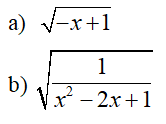
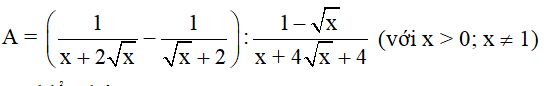
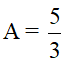
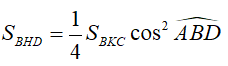


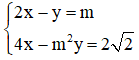

\(P=\left(\frac{2x+1}{\sqrt{x^3}-1}-\frac{\sqrt{x}}{x+\sqrt{x}+1}\right):\left(\frac{3}{\sqrt{x}-1}+\frac{2\sqrt{x}+5}{1-x}\right)\)
\(ĐKXĐ:x\ge0,x\ne1\)
\(P=\frac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\frac{\left(\sqrt{x}+1\right)-\left(2\sqrt{x}+5\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\frac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-2}=\frac{\sqrt{x}+1}{\sqrt{x}-2}\)
b, \(x=\frac{8}{3-\sqrt{5}}=\frac{2\left(9-5\right)}{3-\sqrt{5}}=2\left(3+\sqrt{5}\right)\)
\(=5+2\sqrt{5}+1=\left(\sqrt{5}+1\right)^2\Rightarrow\sqrt{x}=\sqrt{5}+1\)
\(\Rightarrow P=\frac{\sqrt{5}+1+1}{\sqrt{5}+1-2}=\frac{\sqrt{5}+2}{\sqrt{5}-1}\)
c, \(P=\frac{\sqrt{x}-2+3}{\sqrt{x}-2}=1+\frac{3}{\sqrt{x}-2}\in N\)\(\Rightarrow\frac{3}{\sqrt{x}-2}\in Z\)
\(\Rightarrow\sqrt{x}-2\inƯ\left(3\right)\)
\(\Rightarrow x\in\left\{9;25\right\}\)
Bạn ơi, thay x=25/4 vẫn ra P là số tự nhiên nhá, thiếu kìa