tìm x
a,3x+(1x+2)=3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HV
2
DK
1
8 tháng 8 2017
x = -(29997940*i+27069339)/53041780;x = -(10729435*i-30293851)/29983820;x = (10729435*i+30293851)/29983820;x = (29997940*i-27069339)/53041780;
PS
0
DV
2
4 tháng 6 2020
\(D\left(x\right)=-4x^3-4x^3-x^2-x^2+2x+3x+5=0\)
\(-8x^3-2x^2+5x+5=0\)
\(\left(-8x^2-10x-5\right)\left(x-1\right)=0\)
TH1 : \(x=1\)
TH2 : cj phân tích như vậy nhé
\(\Delta=\left(-2\right)^2-4.\left(-8\right).\left(-5\right)=4-160=-156< 0\)
Nên phương trình vô nghiệm (P/s chỗ này : đừng chép vào bài TH2 nhé, cj thử thôi !)
Vậy x = 1
PN
4 tháng 6 2020
\(-4x^3-4x^3-x^2-x^2+2x+3x+5=0\)
\(< =>-8x^3-2x^2+5x+5=0\left(1\right)\)
Nháp : dùng pp nhẩm nghiệm ta thấy \(-8-2+5+5=0\)
Nên phương trình nhận 1 là nghiệm
Dùng lược đồ hóc-ne
-8 1 -8 -2 5 5 -10 -5 0
\(\left(1\right)< =>\left(x-1\right)\left(-8x^2-10x-5\right)=0\)
\(< =>\orbr{\begin{cases}x-1=0\\-8x^2-10x-5=0\end{cases}}\)
\(< =>\orbr{\begin{cases}x=1\\\Delta=\left(-10\right)^2-4.\left(-5\right)\left(-8\right)=100-160=-60\end{cases}}\)
\(< =>\orbr{\begin{cases}x=1\\vo-nghiem\end{cases}}\)
Vậy nghiệm của đa thức trên là 1
TQ
1
TM
16 tháng 4 2021
a, \(x^2\)≥1
\(\Leftrightarrow\) x>1
b, \(x^2\)<1
\(\Rightarrow\) x∈∅
c, \(x^2\)+3x ≥ 0
\(\Leftrightarrow\) \(x^2\)≥-3x
\(\Leftrightarrow\) x≥-3
d, \(x^2\)+3x+3≥0
\(\Leftrightarrow\) \(\left(x+\dfrac{3}{2}\right)^2\)+\(\dfrac{3}{4}\)≥0+\(\dfrac{3}{4}\)
\(\Leftrightarrow\) \(x^2\)+\(\dfrac{3}{2}^2\)≥0
\(\Leftrightarrow\)\(x^2\)≥\(\dfrac{9}{4}\)
\(\Leftrightarrow\)x≥\(\dfrac{3}{2}\)
CM
17 tháng 11 2017
Điều kiện xác định: x ≠ 1; x ≠ 2; x ≠ 3.
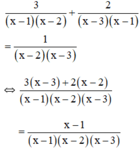
⇒ 3(x – 3) + 2(x – 2) = x – 1
⇔ 3x – 9 + 2x – 4 = x – 1
⇔ 3x + 2x – x = 9 + 4 – 1
⇔ 4x = 12
⇔ x = 3 (không thỏa mãn điều kiện xác định)
Vậy phương trình vô nghiệm.
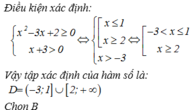
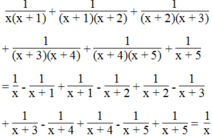
\(3x+\left(1x+2\right)=3\)
\(\Rightarrow3x+x+2=3\)
\(\Rightarrow4x+2=3\)
\(\Rightarrow4x=1\)
\(\Rightarrow x=\frac{1}{4}\)