GIẢI CÁC HỆ PHƯƠNG TRÌNH SAU
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 11 2017
Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
VT = 5.3 – 2.5 = 15 – 10 = 5 = VP
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)
CM
2 tháng 3 2019
Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.
PT
1
PT
1
PT
1
PT
1
PT
1
CM
13 tháng 3 2018
b) x 4 - 5 x 2 + 4 = 0
Đặt t = x 2 ≥ 0 , ta có phương trình:
t 2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t 1 = 1 (nhận) ; t 2 = 4 (nhận)
với t = 1 ⇔ x 2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x 2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
PT
1
CM
21 tháng 4 2017
a) 3 x 2 – 7x + 2 = 0
Δ= 7 2 -4.3.2 = 49 - 24 = 25 > 0 ⇒ ∆ = 5
Phương trình có 2 nghiệm phân biệt:
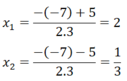
Vậy tập nghiệm của phương trình là S = {2; 1/3}
PT
1
c)\(\left\{{}\begin{matrix}1,5x+0,75y=1\\3x+1,5y=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x+1,5y=2\\3x+1,5y=2\end{matrix}\right.\)
\(\Rightarrow PT\) có vô số nghiệm.
g)\(\left\{{}\begin{matrix}\dfrac{3}{x-2}+\dfrac{2}{y+1}=8\\\dfrac{1}{x-2}+\dfrac{3}{y+1}=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}a=\dfrac{1}{x-2}\\b=\dfrac{1}{y+1}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3a+2b=8\\a+3b=-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3a+2b=8\\3a+9b=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-7b=11\\a=-1-3b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=-\dfrac{11}{7}\\a=\dfrac{26}{7}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x-2}=\dfrac{26}{7}\\\dfrac{1}{y+1}=-\dfrac{11}{7}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{59}{26}\\y=-\dfrac{18}{11}\end{matrix}\right.\)
lần sau em nhớ đăng đúng môn nhé