Giải các bất phương trình, hệ bất phương trình (ẩn m) sau: <img src="http://cdn.hoc24.vn/bk/aEhsFR18pWGS.png" alt="Giải sách bài tập Toán 10 | Giải sbt Toán 10" width="282"...

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:

Khách

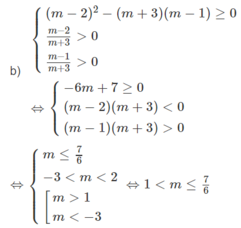
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

25 tháng 11 2019

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:

#Hỏi cộng đồng OLM #Toán lớp 10

Cao Minh Tâm

25 tháng 11 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Nguyễn Hồ Đức Cường

16 tháng 10 2020 - olm

Giải các phương trình:

#Hỏi cộng đồng OLM #Toán lớp 10

Cường Quốc Ngô

8 tháng 8 2016

giải bất phương trìnhtrình

#Hỏi cộng đồng OLM #Toán lớp 10

Cường Quốc Ngô

8 tháng 8 2016

ai đó giải giúp minh với khó quá à

Đúng(0)

1 Nguyễn Hoàng An

17 tháng 9 2021 - olm

: Giải các hệ phương trình

Giúp nhanh vs ạ, đng cần gấp

#Hỏi cộng đồng OLM #Toán lớp 10

Lưu Nguyễn Diễm Phúc

17 tháng 9 2021

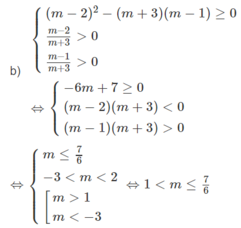
a) Lấy (1)+(2)+(3) là tìm được z rồi thế z vào tìm x, y
b) Lấy (1) + (2) - (3) là tìm được y

Đúng(0)

Hermione Granger

17 tháng 9 2021

\(a)\hept{\begin{cases}x-2y+z=12\\2x-y+3z=18\\-3x+3y+2z=-9\end{cases}\Leftrightarrow\hept{\begin{cases}x-2y+z=12\\3y+z=-6\\6z=21\end{cases}}}\)

\(\text{Đáp số: }(x;y;z)=(\frac{16}{3};-\frac{19}{6};\frac{7}{2})\)

\(b)\hept{\begin{cases}x+y+z=7\\3x-2y+2z=5\\4x-y+3z=10\end{cases}\Leftrightarrow}\hept{\begin{cases}x+y+z=7\\-5y-z=16\\0y+0z=-2\end{cases}}\)

\(\text{ Hệ phương trình vô nghiệm.}\)

Đúng(0)

Sách Giáo Khoa

5 tháng 4 2017

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau :

a) \(2m^2-m-5>0\)

b) \(-m^2+m+9>0\)

#Hỏi cộng đồng OLM #Toán lớp 10

ngonhuminh

6 tháng 4 2017

a) \(2m^2-m-5>0\)(1)

\(\Delta=1+41=42\)Nghiệm của pt (1) là \(\Rightarrow m_1=\dfrac{1-\sqrt{42}}{4};m_2=\dfrac{1+\sqrt{42}}{4}\)

=> nghiệm BPT (1) là:

\(\left[{}\begin{matrix}m< \dfrac{1-\sqrt{42}}{4}\\m>\dfrac{1+\sqrt{42}}{4}\end{matrix}\right.\)

câu b

\(\Delta=1+4.9=37\)Nghiệm pt là \(m_1=\dfrac{1-\sqrt{37}}{2};m_2=\dfrac{1+\sqrt{37}}{2}\)

Nghiệm BPT là: \(\dfrac{1-\sqrt{37}}{2}< m< \dfrac{1+\sqrt{37}}{2}\)

Đúng(0)

Sách Giáo Khoa

5 tháng 4 2017

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau :

a) \(\left(2m-1\right)^2-4\left(m+1\right)\left(m-2\right)\ge0\)

b) \(m^2-\left(2m-1\right)\left(m+1\right)< 0\)

#Hỏi cộng đồng OLM #Toán lớp 10

ngonhuminh

6 tháng 4 2017

\(\Leftrightarrow4m^2-4m+1-4\left(m^2-m-2\right)=9\ge0\Leftrightarrow\forall m\in R\)

\(m^2-\left(2m^2+m-1\right)=-m^2-m+1< 0\)

\(\Leftrightarrow m^2+m-1>0\Rightarrow\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\Rightarrow\left[{}\begin{matrix}m< \dfrac{-1-\sqrt{5}}{2}\\m>\dfrac{-1+\sqrt{5}}{2}\end{matrix}\right.\)

Đúng(0)

ngoc anh

27 tháng 6 2016

Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một mảnh vườn hình chữ nhật có diện tích 720m². Nếu tăng chiều dài thêm 10 m và chiều rộng 6 m thì diện tích mảnh vườn không đổi. Tính chiều dài, chiều rộng mảnh vườn.

#Hỏi cộng đồng OLM #Toán lớp 10

Quốc Đạt

27 tháng 6 2016

undefined

Đúng(0)

Chipu khánh phương

27 tháng 6 2016

...,,,,,,,,,,@ giải một bài toán

Đúng(0)

Thái Minh Hà

27 tháng 7 2016

Toán thi vào lớp 10 đây

Bài 1:

Giải các phương trình và hệ phương trình sau:

a) x² - 8x + 15 = 0.

b) 2x² - √2x - 2 = 0.

c) x⁴ - 5x² - 6 = 0.

#Hỏi cộng đồng OLM #Toán lớp 10

Phùng Khánh Linh

27 tháng 7 2016

Giải các phương trình và hệ phương trình sau:

a) x² - 8x + 15 = 0.

Δ' = 4² - 15 = 1

↔ x = 4 + 1 = 5 hay x = 4 - 1 = 3

b) 2x² - √2x - 2 = 0. (2)

Δ = 2 - 4(2)(-2) = 18

(2) ↔ x = (√2 + 3√2)/4 = √2 hay x = (√2 - 3√2)/4 = -√2/2

c) x⁴ - 5x² - 6 = 0

Đặt u = x² ≥ 0 pt thành:

u² - 5u - 6 = 0 ↔ u = -1 (loại) hay u = 6

Do đó pt ↔ x² = 6 ↔ x = ±√6.

Đúng(0)

Sách Giáo Khoa

5 tháng 4 2017

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau :

a) \(\left\{{}\begin{matrix}2m-1>0\\m^2-\left(m-2\right)\left(2m-1\right)< 0\end{matrix}\right.\)

b) \(\left\{{}\begin{matrix}m^2-m-2< 0\\\left(2m-1\right)^2-4\left(m^2-m-2\right)\le0\end{matrix}\right.\)

#Hỏi cộng đồng OLM #Toán lớp 10

ngonhuminh

5 tháng 4 2017

a)\(\left\{{}\begin{matrix}2m-1>0\Rightarrow m>\dfrac{1}{2}\left(1\right)\\m^2-\left(m-2\right)\left(2m-1\right)< 0\left(2\right)\end{matrix}\right.\)

\(\left(2\right)\Leftrightarrow m^2-\left(2m^2-m-4m+2\right)=-m^2+5m-2< 0\)

\(m^2-5m+2>0\Rightarrow\left[{}\begin{matrix}m< \dfrac{5-\sqrt{17}}{2}< \dfrac{1}{2}\\m>\dfrac{5+\sqrt{17}}{2}\end{matrix}\right.\)

Nghiệm hệ là

\(m>\dfrac{5+\sqrt{17}}{2}\)

b)\(\left\{{}\begin{matrix}m^2-m-2< 0\left(1\right)\\\left(2m-1\right)^2-4\left(m^2-m-2\right)\le0\left(2\right)\end{matrix}\right.\)

\(\left(2\right)\left(2m-1\right)^2-4\left(m^2-m-2\right)=9< 0,\forall m\).
Suy ra (2) vô nghiệm .

Kết luận hệ vô nghiệm.

Đúng(0)