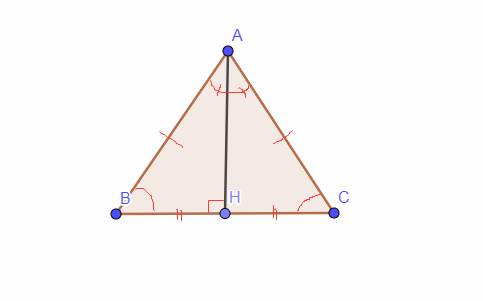
Cho tam giác ABC cân ở A. Vẽ AH \(\perp\) BC (H \(\varepsilon\) BC). Chứng minh rằng:
a) Tam giác AHB = tam giác AHC
b) H là chung điểm của BC
c) AH là tia phân giác của góc BAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2021
a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
22 tháng 10 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của \(\widehat{BAC}\)
c: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
4 tháng 3 2023
`\color{blue}\text {#DuyNam}`
`a,` Vì Tam giác `ABC` cân `-> AB=AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABH` và Tam giác `ACH` có:
\(\widehat{B}=\widehat{C}\)
`AB = AC`
`=>` Tam giác `ABH =` Tam giác `ACH (ch-gn)`
`-> HB=HC (2` cạnh tương ứng `)`
`-> H` là trung điểm của `BC`
`b,` Vì Tam giác `ABH =` Tam giác `ACH (a)`
`->`\(\widehat{BAH}=\widehat{CAH}\) `(2` góc tương ứng `)`
`-> AH` là tia phân giác của \(\widehat{BAC}\)
7 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC,}` $\widehat {B} = \widehat {C}$
Vì `\text {AH}` là đường cao
`-> \text {AH} \bot \text {BC}`
`->` $\widehat {AHB} = \widehat {AHC} = 90^0$
Xét `2 \Delta` vuông `AHB` và `AHC`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
`=> \Delta AHB = \Delta AHC (ch-gn)`
`b,`
Vì `\Delta AHB = \Delta AHC (a)`
`-> \text {HB = HC (2 cạnh tương ứng)}`
`-> \text {H là trung điểm của BC}`
Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)
Vì `\Delta ABC` cân tại A.
Mà `\text {AH}` là đường cao
`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`
`-> \text {AH cũng là đường trung tuyến}`
`-> \text {H là trung điểm của BC}`
`c,`
Vì `\Delta AHB = \Delta AHC (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$
`-> \text {AH là tia phân giác của} \Delta ABC`
Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)
Vì `\Delta ABC` cân tại A.
Mà `\text {AH}` là đường cao
`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`
`-> \text {AH cũng là đường phân giác}`
7 tháng 6 2023
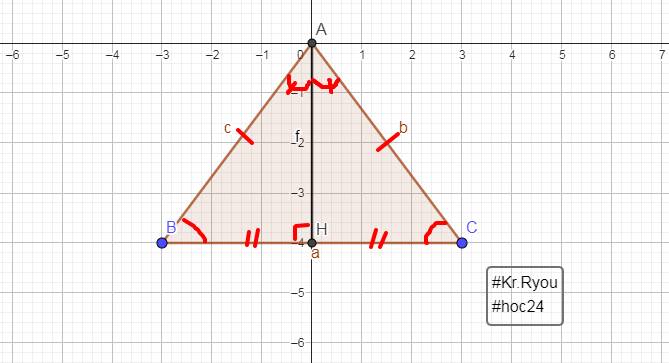
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
c: ΔABC cân tại A
mà AH là trung tuyến
nên AH là phân giác
4 tháng 3 2022
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
b: \(\widehat{BAC}=70^0\)
nên \(\widehat{BAH}=35^0\)
=>\(\widehat{B}=55^0\)
=>BH<AH
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE
hay ΔADE cân tại A
29 tháng 10 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của \(\widehat{BAC}\)
c: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=BC/2=3cm
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2+3^2=5^2\)
=>\(HA^2=25-9=16\)
=>HA=4(cm)
Ta có hình vẽ:
Ta có: AC = AB và góc CAH = BAH (tính chất của Δ cân)
Cách 1: Xét Δ AHB và Δ AHC có:
AB = AC (gt)
BAH = CAH (chứng minh trên)
AH là cạnh chung
Do đó, Δ AHB = Δ AHC (c.g.c) (đpcm)
Cách 2: Vì AH⊥BC⇒AHC=AHB=90oAH⊥BC⇒AHC=AHB=90o
Xét Δ AHB và Δ AHC có:
CAH = BAH (chứng minh trên)
AB = AC (gt)
AHC = AHB (chứng minh trên)
Do đó, Δ AHB = Δ AHC (g.c.g) (đpcm)
bạn ơi cái này là tam giác vuông mà